题目内容
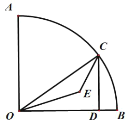
【题目】如图1,在△ABC中,I是内心,AB=AC,O是AB边上一点,以点O为圆心,OB为半径的⊙O经过点I.
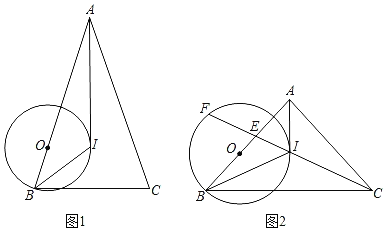
(1)求证:AI是⊙O的切线;
(2)如图2,连接CI交AB于点E,交⊙O于点F,若tan∠IBC=![]() ,求
,求![]() .
.
【答案】(1)证明见解析;(2)![]() =
=![]() .
.
【解析】
(1)延长AI交BC于D,连接OI.由I是△ABC的内心,得到BI平分∠ABC,AI平分∠BAC.求得∠1=∠3,推出OI∥BD,得到OI⊥AI.于是得到结论;
(2)连接BF,过B作BM⊥CF于M由(1)得AD垂直平分BC,求得BI=CI,根据等腰三角形的性质得到∠1=∠4,设法证得FB∥AD,证得△AEI~△BEF,得到![]() .设ID=a,求得
.设ID=a,求得![]() ,根据三角函数的定义即可得到结论.
,根据三角函数的定义即可得到结论.
(1)证明:延长AI交BC于D,连接OI.

∵I是△ABC的内心,
∴BI平分∠ABC,AI平分∠BAC.
∴∠1=∠3,
∵AB=AC,
∴AD⊥BC.
又∵OB=OI,
∴∠3=∠2.
∴∠1=∠2.
∴OI∥BD,
∴OI⊥AI,
∴AI为⊙O的切线;
(2)解:连接BF,过B作BM⊥CF于M,
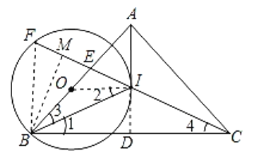
由(1)得AD垂直平分BC,
∴BI=CI,
∴∠1=∠4
故∠1=∠2=∠3=∠4=α,
∴∠BOI=180°﹣2α,
∴∠F=![]() ∠BOI=90°﹣α,
∠BOI=90°﹣α,
∴∠F+∠4=90°,
∴∠FBC=∠ADC=90°,
∴FB∥AD,
∴△BEF~△AEI,
∴![]() .
.
∵DI∥BF,BD=CD,
∴CI=FI,
∴BF=2ID,
故![]() ,
,
设ID=a,
∵![]() ,
,
∴![]() ,
,
由面积法:![]() ,
,
∴![]() ,
,
又∠MIB=2∠1=∠ABD,
∴tan∠MIB=tan∠ABD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴ .
.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目