题目内容
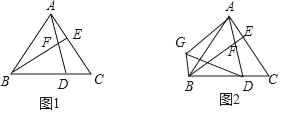
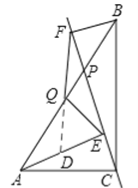
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
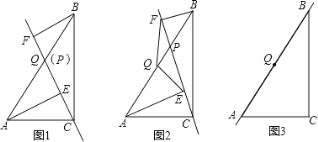
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
【答案】解:(1)AE∥BF,QE=QF。
(2)QE=QF,证明如下:
如图,延长FQ交AE于D,
![]()
∵AE∥BF,∴∠QAD=∠FBQ。
在△FBQ和△DAQ中,∵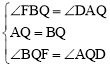 ,
,
∴△FBQ≌△DAQ(ASA)。∴QF=QD。
∵AE⊥CP,∴EQ是直角三角形DEF斜边上的中线。
∴QE=QF=QD,即QE=QF。
(3)(2)中的结论仍然成立。证明如下:
如图,延长EQ、FB交于D,
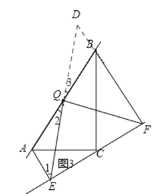
∵AE∥BF,∴∠1=∠D。
在△AQE和△BQD中,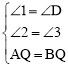 ,
,
∴△AQE≌△BQD(AAS),∴QE=QD。
∵BF⊥CP,∴FQ是斜边DE上的中线。∴QE=QF。
【解析】(1)证△BFQ≌△AEQ即可。理由是:
如图,∵Q为AB中点,∴AQ=BQ。
∵BF⊥CP,AE⊥CP,∴BF∥AE,∠BFQ=∠AEQ。
在△BFQ和△AEQ中,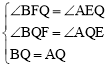 ,∴△BFQ≌△AEQ(AAS)。∴QE=QF。
,∴△BFQ≌△AEQ(AAS)。∴QE=QF。
(2)证△FBQ≌△DAQ,推出QF=QD,根据直角三角形斜边上中线性质求出即可。
(3)证△AEQ≌△BDQ,推出DQ=QE,根据直角三角形斜边上中线性质求出即可。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】下表给出了某班6名同学的身高情况(单位:cm).
学生 | A | B | C | D | E | F | |
身高(单位:cm) | 165 | ____ | 166 | ____ | ____ | 172 | |
身高与班级平 | 均身高的差值) | -1 | +2 | ____ | -3 | +4 | ____ |
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6名同学身高的达标率是多少?
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天的生产量与计划量相比有出入。下表是某周的生产情况(超产为正,减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +4 | -2 | -5 | +13 | -11 | +17 | -9 |
(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比产量最少的一天多生产 辆;
(3)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖6元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?