题目内容
【题目】如图,已知A(a,m)、B(2a,n)是反比例函数y=![]() (k>0)与一次函数y=-
(k>0)与一次函数y=-![]() x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.
x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.
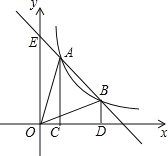
【答案】2≤S△OAB≤8.
【解析】
试题分析:先根据函数图象上点的坐标特征得出m=![]() ,n=
,n=![]() ,
,![]() =-
=-![]() a+b,
a+b,![]() =-
=-![]() a+b,于是k=
a+b,于是k=![]() a2,再由反比例函数系数k的几何意义可知S△OAC=S△OBD,那么S△OAB=S△OAC-S△OBD+S梯形ABDC=S梯形ABDC=2a2,根据二次函数的性质即可求解.
a2,再由反比例函数系数k的几何意义可知S△OAC=S△OBD,那么S△OAB=S△OAC-S△OBD+S梯形ABDC=S梯形ABDC=2a2,根据二次函数的性质即可求解.
试题解析:∵A(a,m)、B(2a,n)在反比例函数y=![]() (k>0)的图象上,
(k>0)的图象上,
∴m=![]() ,n=
,n=![]() ,
,
∵A(a,m)、B(2a,n)在一次函数y=-![]() x+b图象上,
x+b图象上,
∴![]() =-
=-![]() a+b,
a+b,![]() =-
=-![]() a+b,
a+b,
解得:k=![]() a2,
a2,
∴S△OAB=S△OAC-S△OBD+S梯形ABDC
=S梯形ABDC
=![]() (
(![]() +
+![]() )(2a-a)
)(2a-a)
=![]() ×
×![]() ×a
×a
=![]() k
k
=![]() ×
×![]() a2
a2
=2a2.
当1≤a≤2时,S△OAB=2a2,随自变量的增大而增大,此时2≤S△OAB≤8.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目