题目内容
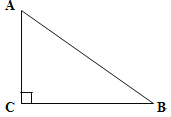
【题目】如图,△ABC中,AB=AC,∠BAC=90°,D是BC边上任意一点,求证：BD
+CD=2AD.
【答案】见解析
【解析】
作AE⊥BC于E，由于∠BAC=90°，AB=AC，所以BE=CE，要证明BD
+CD=2AD，只需找出BD、CD、AD三者之间的关系即可，由勾股定理可得出AD=AE+ED，AE=AB-BE=AC-CE，ED=BD-BE=CE-CD，代入求出三者之间的关系即可得证．
证明：作AE⊥BC于E，如图所示：
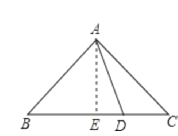
由题意得：ED=BDBE=CECD，
∵在△ABC中,∠BAC=90°，AB=AC，
∴BE=CE=
BC，
由勾股定理可得：
AB+AC=BC，
AE=ABBE=ACCE，，
AD=AE+ED，
2ADimg src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/22/06/793bb150/SYS202011220603314423751839_DA/SYS202011220603314423751839_DA.001.png" width="11" height="20" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />=2AE+2ED=ABBE+(BDBE) +ACCE+(CECD)
=AB+AC+BD+CD2BD×BE2CD×CE=AB+AC+BD+CD2×BC×BC
=BD+CD,
即,BD+CD=2AD
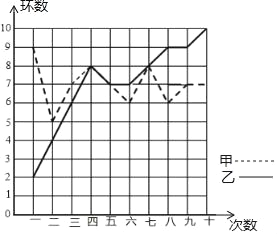
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次，每次射耙的成绩情况如图所示：
（1）请将下表补充完整：（参考公式：方差S2=
[（x1﹣
）2+（x2﹣）2+…+（xn﹣）2]）
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
（2）请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看， 的成绩好些；
②从平均数和中位数相结合看， 的成绩好些；
③若其他队选手最好成绩在9环左右，现要选一人参赛，你认为选谁参加，并说明理由．
