��Ŀ����
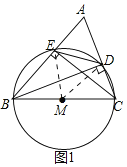
����Ŀ��(1)����������տư桶��ѧ�����꼶(�ϲ�)ϰ��2.1������һ����ϰ�⣺��ͼ�٣�BD��CE�ǡ�ABC�ĸߣ�M��BC���е㣬��B��C��D��E�Ƿ����Ե�MΪԲ�ĵ�ͬһ��Բ�ϣ�Ϊʲô��
�ڽ������ʱ������Ҫ˵������B��C��D��E���Ե�MΪԲ�ĵ�ͬһ��Բ�ϡ���������MD��ME�Ļ����ϣ�ֻ��֤���� ��
(2)����˼������ͼ�ڣ�BD��CE����ǡ�ABC�ĸߣ�����DE����֤����ADE����ABC��С���ڽ�����ʱ�������ˡ�Բ���ڽ��ı��εĶԽǻ���������֤����(�������С����˼·���֤�����̣�)
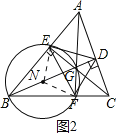
(3)�ƹ����ã���ͼ�ۣ�BD��CE��AF����ǡ�ABC�ĸߣ������ߵĽ���G������ABC�Ĵ��ģ�����DE��EF��FD����֤����G�ǡ�DEF�����ģ�
���𰸡�(1)ME��MD��MB��MC��(2)֤����������(3)֤����������
��������
(1)Ҫ֤�ĸ�����ͬһԲ�ϣ���֤���ĸ��㵽���������ȣ�
(2)�ɡ�ֱ��������б���ϵ����ߵ���б�ߵ�һ�롱������֤ME��MD��MB��MC���õ��ı���BCDEΪԲ�ڽ��ı��Σ����жԽǻ�����
(3)�������Ķ��壬��֤��DG��EG��FG�ֱ�ƽ�֡�EDF����DEF����DFE���ɵ�B��C��D��E�ĵ㹲Բ���ɵ�ͬ�����Ե�Բ�ܽǡ�CBD����CED������Ϊ��BEG����BFG��90�㣬����(2)��֤��B��F��G��EҲ�ĵ㹲Բ����ͬ�����Ե�Բ�ܽǡ�FBG����FEG�����������С�CED����FEG��ͬ����֤���������ڽǵ�ƽ���ߣ�
�⣺(1)����Բ�Ķ����֪������B��C��D��E����M�������ʱ����������ԲM��
�ʴ�Ϊ��ME��MD��MB��MC
(2)֤��������MD��ME
��BD��CE�ǡ�ABC�ĸ�
��BD��AC��CE��AB
���BDC����CEB��90��
��MΪBC���е�
��ME��MD��![]() BC��MB��MC
BC��MB��MC
���B��C��D��E���Ե�MΪԲ�ĵ�ͬһ��Բ��
���ABC+CDE��180��
�ߡ�ADE+��CDE��180��
���ADE����ABC
(3)֤����ȡBG�е�N������EN��FN
��CE��AF�ǡ�ABC�ĸ�
���BEG����BFG��90��
��EN��FN��![]() BG��BN��NG
BG��BN��NG
���B��F��G��E���Ե�NΪԲ�ĵ�ͬһ��Բ��
���FBG����FEG
����(2)֤�õ�B��C��D��E��ͬһ��Բ��
���FBG����CED
���FEG����CED
ͬ����֤����EFG����AFD����EDG����FDG
���G�ǡ�DEF������