题目内容
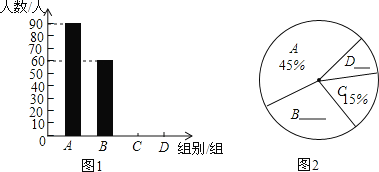
【题目】某中学举行“中国梦,我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
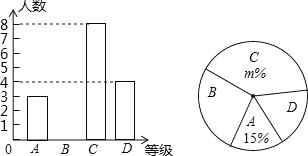
(1)参加比赛的学生共有 名,在扇形统计图中,表示“D等级”的扇形的圆心角为 度,图中m的值为 ;
(2)补全条形统计图;
(3)组委会决定分别从本次比赛中获利A、B两个等级的学生中,各选出1名学生培训后搭档去参加市中学生演讲比赛,已知甲的等级为A,乙的等级为B,求同时选中甲和乙的概率.
【答案】(1)20,72,40;(2)见解析;(3)![]()
【解析】
(1)根据等级为A的人数除以所占的百分比求出总人数,用360°乘以D等级对应比例可得其圆心角度数,根据百分比的概念可得m的值;
(2)求出等级B的人数,补全条形统计图即可;
(3)列表得出所有等可能的情况数,找出符合条件的情况数,即可求出所求的概率.
解:(1)根据题意得:3÷15%=20(人),
表示“D等级”的扇形的圆心角为![]() ×360°=72°;
×360°=72°;
C级所占的百分比为![]() ×100%=40%,
×100%=40%,
故m=40,
故答案为:20,72,40.
(2)等级B的人数为20-(3+8+4)=5(人),
补全统计图,如图所示:

(3)列表如下:
乙 | B | B | B | B | |
甲 | 甲、乙 | 甲、B | 甲、B | 甲、B | 甲、B |
A | A、乙 | A、B | A、B | A、B | A、B |
A | A、乙 | A、B | A、B | A、B | A、B |
所有等可能的结果有15种,同时选中甲和乙的情况有1种,
所以同时选中甲和乙的概率为![]() .
.

【题目】雾霾天气严重影响人民的生活质量.在今年“元旦”期间,某校九(1)班的综合实践小组同学对“雾霾天气的主要成因”随机调查了本地部分市民,并对调查结果进行了整理,绘制了如图不完整的统计图表,观察分析并回答下列问题.
组别 | 雾霾天气的主要成因 |
A | 工业污染 |
B | 汽车尾气排放 |
C | 炉烟气排放 |
D | 其他(滥砍滥伐等) |
(1)本次被调查的市民共有多少人?
(2)分别补全条形统计图和扇形统计图;
(3)若该地区有100万人口,请估计持有A、B两组主要成因的市民有多少人?