题目内容
11.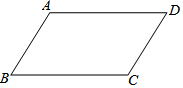 如图,平行四边形ABCD中,AD>AB
如图,平行四边形ABCD中,AD>AB(1)分别作∠ABC和∠BCD的平分线,交AD于E、F.
(2)线段AF与DE相等吗?请证明.
分析 由平行四边形ABCD的对边平行且相等、平行线的性质、角平分线的定义推知∠ABE=∠AEB,则AE=AB,∠DCF=∠DFC,则DF=DC,故AF=DE.
解答 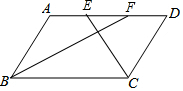 解:AF与DE相等.理由如下:
解:AF与DE相等.理由如下:
∵四边形ABCD是平行四边形,
∴AB=DC,AD=BC.
∵AD∥BC,BE平分∠ABC,
∴∠ABE=∠AEB,
∴AE=AB.
∵CF平分∠BCD,
∴∠DCF=∠FCB,
∴∠DCF=∠DFC,
∴DF=DC,
∴AF=DE.
点评 本题考查了平行四边形的性质.解题时,将所求的线段间的数量关系,转化为推知角、角关系,充分利用了等腰三角形的判定与性质.

练习册系列答案
相关题目
2.下列方程中,有两个不相等的实数根的是( )
| A. | x2+2017=0 | B. | (x+2017)2=0 | C. | (x+1)2=-2017 | D. | (x+2017)(x-2017)=0 |
3.一元二次方程mx2-2x+1=0总有实数根,则m应满足的条件是( )
| A. | m>1 | B. | m≤1 | C. | m<1且 m≠0 | D. | m≤1且 m≠0 |
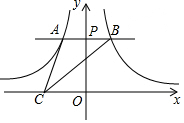 如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数$y=-\frac{3}{x}$和$y=\frac{1}{x}$的图象交于A点和B点,若点C为x轴上任意一点,连接AC、BC,则△ABC的面积为2.
如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数$y=-\frac{3}{x}$和$y=\frac{1}{x}$的图象交于A点和B点,若点C为x轴上任意一点,连接AC、BC,则△ABC的面积为2.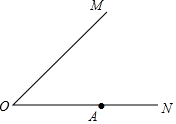 已知:如图,∠MON及边ON上一点A.在∠MON内部求作:点P,使得PA⊥ON,且点P 到∠MON两边的距离相等.(请用尺规作图,保留作图痕迹,不要求写出作法,不必证明).
已知:如图,∠MON及边ON上一点A.在∠MON内部求作:点P,使得PA⊥ON,且点P 到∠MON两边的距离相等.(请用尺规作图,保留作图痕迹,不要求写出作法,不必证明).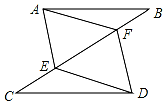 已知△ABF≌△DCE,E与F是对应顶点.证明AF∥DE.
已知△ABF≌△DCE,E与F是对应顶点.证明AF∥DE.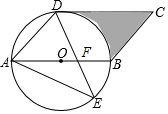 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,若⊙O的半径为6cm,且∠AED=45°.
如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,若⊙O的半径为6cm,且∠AED=45°.