ΧβΡΩΡΎ»ί
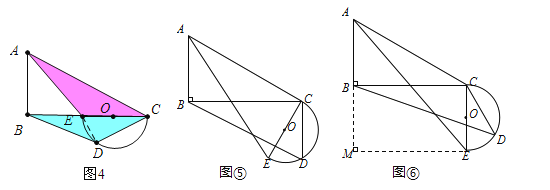
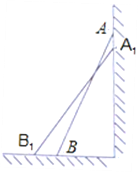
ΓΨΧβΡΩΓΩΤΫΟφ…œΘ§RtΓςABC”κ÷±ΨΕΈΣCEΒΡΑκ‘≤O»γΆΦ1ΑΎΖ≈Θ§ΓœB=90ΓψΘ§AC=2CE=mΘ§BC=nΘ§Ακ‘≤OΫΜBC±Ώ”ΎΒψDΘ§ΫΪΑκ‘≤O»ΤΒψCΑ¥Ρφ ±’κΖΫœρ–ΐΉΣΘ§ΒψDΥφΑκ‘≤O–ΐΉΣ«“ΓœECD Φ÷’Β»”ΎΓœACBΘ§–ΐΉΣΫ«Φ«ΈΣΠΝΘ®0ΓψΓήΠΝΓή180ΓψΘ©Θ°
Θ®1Θ©Β±ΠΝ=0Γψ ±Θ§Ν§Ϋ”DEΘ§‘ρΓœCDE=ΓΓ ΓΓΓψΘ§CD=ΓΓ ΓΓΘΜ
Θ®2Θ© ‘≈–ΕœΘΚ–ΐΉΣΙΐ≥Χ÷–![]() ΒΡ¥σ–Γ”–Έό±δΜ·ΘΩ«κΫωΨΆΆΦ2ΒΡ«ι–ΈΗχ≥ω÷ΛΟςΘΜ
ΒΡ¥σ–Γ”–Έό±δΜ·ΘΩ«κΫωΨΆΆΦ2ΒΡ«ι–ΈΗχ≥ω÷ΛΟςΘΜ
Θ®3Θ©»τm=10Θ§n=8Θ§Β±–ΐΉΣΒΡΫ«Ε»ΠΝ«ΓΈΣΓœACBΒΡ¥σ–Γ ±Θ§«σœΏΕΈBDΒΡ≥ΛΘΜ
Θ®4Θ©»τm=6Θ§n=![]() Θ§Β±Ακ‘≤O–ΐΉΣ÷Ν”κΓςABCΒΡ±Ώœύ«– ±Θ§÷±Ϋ”–¥≥ωœΏΕΈBDΒΡ≥ΛΘ°
Θ§Β±Ακ‘≤O–ΐΉΣ÷Ν”κΓςABCΒΡ±Ώœύ«– ±Θ§÷±Ϋ”–¥≥ωœΏΕΈBDΒΡ≥ΛΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©90Θ§![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() Θ§Έό±δΜ·Θ§Θ®3Θ©BD=
Θ§Έό±δΜ·Θ§Θ®3Θ©BD=![]() ΘΜΘ®4Θ©Φ¥ΘΚBD=
ΘΜΘ®4Θ©Φ¥ΘΚBD=![]() Μρ
Μρ![]() Θ°
Θ°
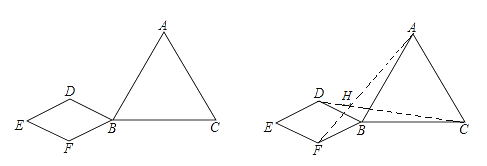
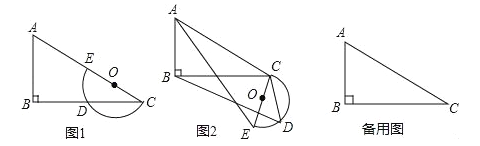
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΔΌΗυΨί÷±ΨΕΒΡ–‘÷ Θ§”…DEΓΈABΒΟ![]() Φ¥Ω…ΫβΨωΈ ΧβΘ°ΔΎ«σ≥ωBDΓΔAEΦ¥Ω…ΫβΨωΈ ΧβΘ°
Φ¥Ω…ΫβΨωΈ ΧβΘ°ΔΎ«σ≥ωBDΓΔAEΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®2Θ©÷Μ“Σ÷ΛΟςΓςACEΓΉΓςBCDΦ¥Ω…Θ°
Θ®3Θ©«σ≥ωABΓΔAEΘ§άϊ”ΟΓςACEΓΉΓςBCDΦ¥Ω…ΫβΨωΈ ΧβΘ°
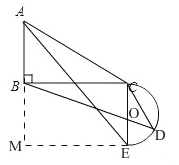
Θ®4Θ©Ζ÷άύΧ÷¬έΘΚΔΌ»γΆΦ5÷–Θ§Β±ΠΝ=90Γψ ±Θ§Ακ‘≤”κACœύ«–Θ§ΔΎ»γΆΦ6÷–Θ§Β±ΠΝ=90Γψ+ΓœACB ±Θ§Ακ‘≤”κBCœύ«–Θ§Ζ÷±π«σ≥ωBDΦ¥Ω…Θ°
‘ΧβΫβΈωΘΚΘ®1Θ©ΫβΘΚΔΌ»γΆΦ1÷–Θ§Β±ΠΝ=0 ±Θ§Ν§Ϋ”DEΘ§‘ρΓœCDE=90ΓψΘ°ΓΏΓœCDE=ΓœB=90ΓψΘ§ΓύDEΓΈABΘ§Γύ![]() =
=![]() Θ°ΓΏBC=nΘ§ΓύCD=
Θ°ΓΏBC=nΘ§ΓύCD=![]() Θ°Ι ¥πΑΗΈΣΘΚ90ΓψΘ§
Θ°Ι ¥πΑΗΈΣΘΚ90ΓψΘ§![]() nΘ°
nΘ°
ΔΎ»γΆΦ2÷–Θ§Β±ΠΝ=180Γψ ±Θ§BD=BC+CD=![]() nΘ§AE=AC+CE=
nΘ§AE=AC+CE=![]() mΘ§Γύ
mΘ§Γύ![]() =
=![]() Θ°Ι ¥πΑΗΈΣΘΚ
Θ°Ι ¥πΑΗΈΣΘΚ![]() Θ°
Θ°
Θ®2Θ©»γΆΦ3÷–Θ§ΓΏΓœACB=ΓœDCEΘ§ΓύΓœACE=ΓœBCDΘ°ΓΏ![]() Θ§ΓύΓςACEΓΉΓςBCDΘ§Γύ
Θ§ΓύΓςACEΓΉΓςBCDΘ§Γύ![]() Θ°
Θ°
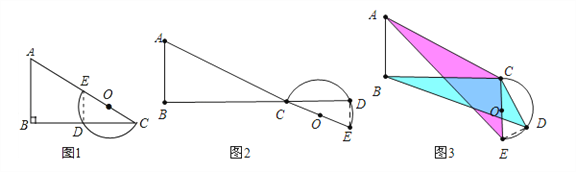
Θ®3Θ©»γΆΦ4÷–Θ§Β±ΠΝ=ΓœACB ±Θ°‘ΎRtΓςABC÷–Θ§ΓΏAC=10Θ§BC=8Θ§ΓύAB=![]() =6Θ°‘ΎRtΓςABE÷–Θ§ΓΏAB=6Θ§BE=BC©¹CE=3Θ§ΓύAE=
=6Θ°‘ΎRtΓςABE÷–Θ§ΓΏAB=6Θ§BE=BC©¹CE=3Θ§ΓύAE=![]() =
=![]() =3
=3![]() Θ§”…Θ®2Θ©Ω…÷ΣΓςACEΓΉΓςBCDΘ§Γύ
Θ§”…Θ®2Θ©Ω…÷ΣΓςACEΓΉΓςBCDΘ§Γύ![]() Θ§Γύ
Θ§Γύ![]() =
=![]() Θ§ΓύBD=
Θ§ΓύBD=![]() Θ°Ι ¥πΑΗΈΣΘΚ
Θ°Ι ¥πΑΗΈΣΘΚ![]() Θ°
Θ°
Θ®4Θ©ΓΏm=6Θ§n=![]() Θ§ΓύCE=3Θ§CD=2
Θ§ΓύCE=3Θ§CD=2![]() Θ§AB=
Θ§AB=![]() =2Θ§ΔΌ»γΆΦ5÷–Θ§Β±ΠΝ=90Γψ ±Θ§Ακ‘≤”κACœύ«–Θ°‘ΎRtΓςDBC÷–Θ§BD=
=2Θ§ΔΌ»γΆΦ5÷–Θ§Β±ΠΝ=90Γψ ±Θ§Ακ‘≤”κACœύ«–Θ°‘ΎRtΓςDBC÷–Θ§BD=![]() =
=![]() =2
=2![]() Θ°
Θ°
ΔΎ»γΆΦ6÷–Θ§Β±ΠΝ=90Γψ+ΓœACB ±Θ§Ακ‘≤”κBCœύ«–Θ§ΉςEMΓΆAB”ΎMΘ°ΓΏΓœM=ΓœCBM=ΓœBCE=90ΓψΘ§ΓύΥΡ±Ώ–ΈBCEM «ΨΊ–ΈΘ§Γύ![]() Θ§ΓύAM=5Θ§AE=
Θ§ΓύAM=5Θ§AE=![]() =
=![]() Θ§”…Θ®2Θ©Ω…÷Σ
Θ§”…Θ®2Θ©Ω…÷Σ![]() =
=![]() Θ§ΓύBD=
Θ§ΓύBD=![]() Θ°
Θ°
Ι ¥πΑΗΈΣΘΚ2![]() Μρ
Μρ![]() Θ°
Θ°