题目内容
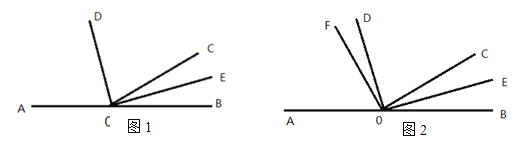
【题目】如图1,已知A、O、B三点在同一直线上,射线OD、OE分别平分∠AOC、∠BOC
(1)求∠DOE的度数;
(2)如图2,在∠AOD内引一条射线OF,使∠COF=![]() ,其他不变,设∠DOF=
,其他不变,设∠DOF=![]()
![]() )
)
①求∠AOF的度数(用含![]() 的代数式表示).
的代数式表示).
②若∠BOD是∠AOF的2倍,求∠DOF的度数.
【答案】(1) ∠DOE=![]() (2) ∠AOF=
(2) ∠AOF=![]() ;(3)
;(3)![]()
【解析】
(1)根据角平分线的性质解答即可;(2)①根据互余解答即可;②根据∠BOD是∠AOF的2倍,列方程可得α的值.
(1)∵点A,O,B在同一条直线上,
∴∠AOC+∠BOC=180°,
∵射线OD和射线OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠COD+∠COE=![]() (∠AOC+∠BOC)=90°,
(∠AOC+∠BOC)=90°,
∴∠DOE=90°;
(2)①∵OC⊥OF,
∴∠COF=90°,
∵∠DOF=αo,
∴∠COD=90°-α°,
∵∠AOD=∠COD,
∴∠AOF=∠AOD-∠DOF=90°-α°-α°=(90-2α)°,
②∵∠BOD是∠AOF的2倍,
∴180°-(90-α)°=2(90-2α)°,
α=18°,
即∠DOF=18°.

练习册系列答案
相关题目