题目内容
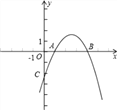
【题目】已知,抛物线y=ax2+bx-2与x轴的两个交点分别为A(1,0),B(4,0),与y轴的交点为C.
(1)求出抛物线的解析式及点C的坐标;
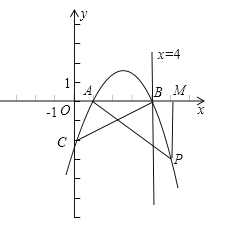
(2)点P是在直线x=4右侧的抛物线上的一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OCB相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2+
x2+![]() x-2;(2)见解析
x-2;(2)见解析
【解析】试题分析:(1)由A和B两点在抛物线上,故把两点坐标代入抛物线解析式中,得到关于a与b的方程组,求出方程组的解即可得到a与b的值,从而确定出抛物线解析式,然后令求出的解析式中x=0,求出y的值即为C的纵坐标,写出C的坐标即可;
(2)存在P点,使得以A,P,M为顶点的三角形与△OCB相似,理由为:根据题意画出图形,如图所示,根据题意分别求出OA,OB及OC的长,设出P点的横坐标为m,代入抛物线解析式表示出纵坐标,因纵坐标为负值,求出其纵坐标的相反数即为PM的长,且用OM﹣OA表示出AM的长,若三角形相似,根据对应点对应不同分两种情况,由相似三角形对应边成比例列出关于m的方程,分别求出方程的解即可得到m的值,从而确定出P的坐标.
试题解析:解:(1)把A(1,0)和B(4,0)代入抛物线解析式得:
![]() ,②﹣①×4得:12a=﹣6,解得:a=﹣
,②﹣①×4得:12a=﹣6,解得:a=﹣![]() ,把a=﹣
,把a=﹣![]() 代入①,解得:b=
代入①,解得:b=![]() ,所以方程组的解为:
,所以方程组的解为: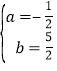 ,∴抛物线解析式为y=﹣
,∴抛物线解析式为y=﹣![]() x2+
x2+![]() x﹣2,令x=0,解得y=2,则C的坐标为(0,﹣2);
x﹣2,令x=0,解得y=2,则C的坐标为(0,﹣2);
(2)存在.根据题意画出图形,如图所示,设P的坐标为(m,﹣![]() m2+
m2+![]() m﹣2)(m>4),根据题意得:OA=1,OC=2,OB=4,则PM=
m﹣2)(m>4),根据题意得:OA=1,OC=2,OB=4,则PM=![]() m2﹣
m2﹣![]() m+2,MA=MO﹣OA=m﹣1,若△BOC∽△AMP,∴
m+2,MA=MO﹣OA=m﹣1,若△BOC∽△AMP,∴![]() =
=![]() ,即
,即![]() =
=![]() ,化简得:m2﹣6m+5=0,即(m﹣1)(m﹣5)=0,解得:m1=1(舍去),m2=5,则P坐标为(5,﹣2);
,化简得:m2﹣6m+5=0,即(m﹣1)(m﹣5)=0,解得:m1=1(舍去),m2=5,则P坐标为(5,﹣2);
若△BOC∽△PMA,∴![]() =
=![]() ,即
,即![]() =
=![]() ,化简得:m2﹣9m+8=0,即(m﹣1)(m﹣8)=0,解得:m1=1(舍去),m2=8,则P的坐标为(8,﹣14).
,化简得:m2﹣9m+8=0,即(m﹣1)(m﹣8)=0,解得:m1=1(舍去),m2=8,则P的坐标为(8,﹣14).
综上所述:满足题意的P有两个,其坐标分别为(5,﹣2)或(8,﹣14).

 名校课堂系列答案
名校课堂系列答案