题目内容
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧 ![]() 于点D,连接CD、OD.下列结论:①AC∥OD;②CE=OE;③∠OED=∠AOD;④CD=DE.其中正确结论的个数有( )
于点D,连接CD、OD.下列结论:①AC∥OD;②CE=OE;③∠OED=∠AOD;④CD=DE.其中正确结论的个数有( ) 
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解:①∵AB是半圆直径, ∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO= ![]() ∠CAB,
∠CAB,
∴∠CAD=∠ADO,
∴AC∥OD,
∴①正确.②过点E作EF⊥AC,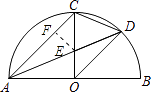
∵OC⊥AB,AD平分∠CAB交弧BC于点D,
∴OE=EF,
在Rt△EFC中,CE>EF,
∴CE>OE,
∴②错误.③∵在△ODE和△ADO中,
∠DEO=90°+∠DAO,
∠AOD=90°+∠COD,
∵∠DAO= ![]() ∠COD,
∠COD,
∴③∠OED=∠AOD错误;④作ON⊥CD,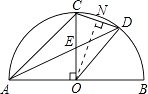
∵AD平分∠CAB交弧BC于点D,
∴∠CAD= ![]() ×45°=22.5°,
×45°=22.5°,
∴∠COD=45°,
∵AB是半圆直径,
∴OC=OD,
∴∠OCD=∠ODC=67.5°,
∠AEO=90°﹣22.5°=67.5°,
∴∠DCE=∠CED=67.5°,
∴CD=DE,
∴④正确.
综上所述,只有①④正确.
故选:B.
【考点精析】认真审题,首先需要了解垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧),还要掌握圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)的相关知识才是答题的关键.

【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?






