题目内容
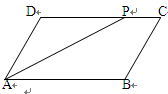
(10分)如图,已知 E、F是四边形ABCD的对角线AC上的两点,AF="CE," DF="BE," DF‖BE。

(1) 试说明△AFD≌△CEB;
(2)试说明四边形ABCD是平行四边形。




(1) 试说明△AFD≌△CEB;
(2)试说明四边形ABCD是平行四边形。




(1)∵DF∥BE, ∴∠DFA="BEC," ∵DF="BE,AF=CE,"
∴△AFD≌△CEB
(2) ∵△AFD≌△CEB, ∴AD="CB," ∠DAF=∠BCE, ∴AD∥CB,
∴四边形ABCD是平行四边形
∴△AFD≌△CEB
(2) ∵△AFD≌△CEB, ∴AD="CB," ∠DAF=∠BCE, ∴AD∥CB,
∴四边形ABCD是平行四边形
试题分析:根据平行线的性质
∵DF∥BE, ∴∠DFA=BEC,根据题目已知 ∵DF="BE,AF=CE,"
∴△AFD≌△CEB(SAS)
(2) ∵△AFD≌△CEB, ∴AD="CB," ∠DAF=∠BCE, ∴AD∥CB,
根据平形四边形的性质得出,四边形ABCD是平行四边形
点评:难度系数中等,考查了考生是否熟练掌握性质定理和判定定理,运用平行线的性质得到相关的线段、角线段,从而证明全等这些考点是中考最常见的。

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 ABCD中,若AB=3cm,AD=5cm,则
ABCD中,若AB=3cm,AD=5cm,则 ,AC、BD相交于点O,
,AC、BD相交于点O, 交AD于点E,则△ABE的周长为( )
交AD于点E,则△ABE的周长为( )


 ,它的周长是
,它的周长是 ,则它的中位线长为 ㎝.
,则它的中位线长为 ㎝. ,求BC的长.
,求BC的长.