题目内容
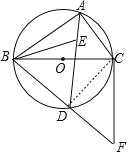
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD![]() DF,连接CF、BE.
DF,连接CF、BE.
(1)求证:DB![]() DE;
DE;
(2)求证:直线CF为⊙O的切线;
(3)若CF![]() 4,求图中阴影部分的面积.
4,求图中阴影部分的面积.

【答案】(1)(2)见解析;(3)![]()
【解析】分析:(1)欲证明DB=DE.,只要证明∠DBE=∠DEB;
(2)欲证明CF是⊙O的切线.,只要证明BC⊥CF即可;
![]() 根据S阴影部分
根据S阴影部分![]() S扇形
S扇形![]() S△OBD计算即可.
S△OBD计算即可.
详解:(1)证明:∵E是△ABC的内心,
∴∠BAE=∠CAE,∠EBA=∠EBC,
∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,
∴∠DBE=∠DEB,
∴DB=DE.
(2)连接CD.
∵DA平分∠BAC,
∴∠DAB=∠DAC,
∴BD=CD,
又∵BD=DF,
∴CD=DB=DF,
∴![]()
∴BC⊥CF,
∴CF是⊙O的切线.
(3)连接OD.
∵O、D是BC、BF的中点,CF![]() 4, ∴OD
4, ∴OD![]() 2.
2.
∵CF是⊙O的切线,
∴![]()
∴△BOD为等腰直角三角形.
∴S阴影部分![]() S扇形
S扇形![]() S△OBD
S△OBD![]()
![]() .
.

练习册系列答案
相关题目
【题目】某客运站行车时刻表如图,若全程保持匀速行驶,则当快车出发______小时后,两车相距25km.
哈尔滨—长春 | 出发时间 | 到站时间 | 里程(km) |
普通车 | 7:00 | 11:00 | 300 |
快车 | 7:30 | 10:30 | 300 |




