题目内容
【题目】(1)如图1,![]() 为正方形
为正方形![]() 的边
的边![]() 上一点,将正方形
上一点,将正方形![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,连接并延长
处,连接并延长![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,点![]() 分别在
分别在![]() 边上,且
边上,且![]() ,求证:
,求证:![]()
(3)如图3,点![]() 分别在
分别在![]() 边上,点
边上,点![]() 分别在
分别在![]() 边上,
边上,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1)见解析;(2)见解析;(3)MN=2 ![]() .
.
【解析】
(1) 连接AF,根据正方形的性质和折叠性质可证明Rt△AGF≌Rt△ADF(HL),从而求得结果DF=GF;(2)属于半角型问题,延长CD至点K,使DK=BE,连接AK,再根据正方形的性质证明△ABE≌△ADK(SAS)和△AFE≌△AFK(SAS)即可解答,具体过程见详解;(3)过点A作AE∥MN交BC于点E,作AF∥PQ交CD于点F,目的是平移MN、PQ到直角三角形中,在Rt△ADF中,AD=6,由勾股定理得DF=3,设BE=x,则CE=6-x,EF=3+x,
在△CEF中,由勾股定理得32+(6-x)2=(3+x)2,从而求解.
(1)连接AF,
∵四边形ABCD是正方形,
∴∠BAD=∠B=∠C=∠D=90°,AB=BC=CD=DA,
由折叠可知,∠AGF=∠AGE=∠ABC=90°,AG=AB=AD,
在Rt△AGF和Rt△ADF中
∵ ![]() ,
,
∴Rt△AGF≌Rt△ADF,
∴DF=GF;
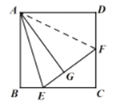
(2)延长CD至点K,使DK=BE,连接AK,
在△ABE和△ADK中
∵  ,
,
∴△ABE≌△ADK,
∴AE=AK,∠EAB=∠KAD,
∴∠KAE=∠BAD=90°,
∵∠EAF=45°,
∴∠KAF=45°=∠EAF,
在△AFE和△AFK中
∵  ,
,
∴△AFE≌△AFK,
∴EF=FK=FD+DK=FD+BE;

(3)过点A作AE∥MN交BC于点E,作AF∥PQ交CD于点F,
则∠EAF=∠MOQ=45°,
由(2)可知EF=BE+DF,
∵AN∥EM,AE∥MN,
∴四边形AEMN为平行四边形,
∴AE=MN,
同理AF=PQ=![]() ,
,
在Rt△ADF中,AD=6,由勾股定理得DF=3,
设BE=x,则CE=6-x,EF=3+x,
在△CEF中,由勾股定理得32+(6-x)2=(3+x)2,
解得,x=2,
再由勾股定理得MN=AE=![]() .
.


 阅读快车系列答案
阅读快车系列答案






