题目内容
【题目】阅读下面材料,完成(1)-(3)题.
数学课上,老师出示了这样一道题:
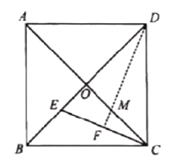
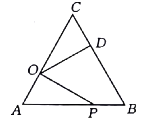
如图,△ABC中,D为BC中点,且AD=AC,M为AD中点,连结CM并延长交AB于N.
探究线段AN、MN、CN之间的数量关系,并证明.
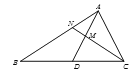
同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现线段AN、AB之间存在某种数量关系.”
小强:“通过倍长不同的中线,可以得到不同的结论,但都是正确的,大家就大胆的探究吧.”
小伟:“通过构造、证明相似三角形、全等三角形,就可以将问题解决.”
......
老师: “若其他条件不变,设AB=a,则可以用含a的式子表示出线段CM的长.”
(1)探究线段AN、AB之间的数量关系,并证明;
(2)探究线段AN、MN、CN之间的数量关系,并证明;
(3)设AB=a,求线段CM的长(用含a的式子表示).
【答案】(1)![]() (2)
(2)![]() 或
或![]() ,证明见解析(3)
,证明见解析(3)![]()
【解析】
(1)过B做BQ∥NC交AD延长线于Q,构造出全等三角形△BDQ≌△CDM(ASA)、相似三角形△ANM∽△ABQ,再利用全等和相似的性质即可得出结论![]() ;
;
(2)延长AD至H,使AD=DH,连接CH,可得△ABD≌△HCD(SAS),进一步可证得![]() ,得到
,得到![]() ,然后证明
,然后证明![]() ,即可得到结论:
,即可得到结论:![]() ;延长CM至Q,使QM=CM,连接AQ,延长
;延长CM至Q,使QM=CM,连接AQ,延长![]() 至
至![]() ,使
,使![]() 可得
可得![]() 、四边形
、四边形![]() 为平行四边形,进一步可证得
为平行四边形,进一步可证得![]() ,即可得到结论
,即可得到结论![]() ;
;
(3)在(1)、(2)的基础之上,用含![]() 的式子表示出
的式子表示出![]() 、
、![]() ,从而得出
,从而得出![]() .
.
(1)过B做BQ∥NC交AD延长线于Q,如图:
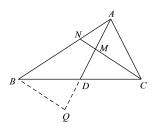
∵D为BC中点
易得△BDQ≌△CDM(ASA)
∴DQ=DM,
∵M为AD中点,
∴AM=DM=DQ,
∵BQ∥NC,
∴△ANM∽△ABQ,
∴![]() ,
,
∴![]() ;
;
(2)①结论:![]() ,
,
证明:延长AD至H,使AD=DH,连接CH,如图:
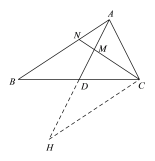
易得△ABD≌△HCD(SAS) ,
∴∠H=∠BAH,
∴AB∥HC,
设AM=x,则AD=AC=2x,AH=4x,
∴![]() ,
,![]() ,
,
∴![]() ;
;
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②结论:![]() ;
;
证明:延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() ,
,
延长![]() 至
至![]() ,使
,使![]() ,如图:
,如图:

则![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)由(1)得,![]() ,
,
∴![]() ,
,
由(2)①得![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】为监控某条生产线上产品的质量,检测员每隔相同时间抽取一件产品,并测量其尺寸(![]() ),在一天的抽检结束后,检测员将测得的各数据按从小到大的顺序整理成如下表格:
),在一天的抽检结束后,检测员将测得的各数据按从小到大的顺序整理成如下表格:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
尺寸 | 8.72 | 8.88 | 8.92 | 8.93 | 8.94 | 8.96 | 8.97 | 8.98 |
| 9.03 | 9.04 | 9.06 | 9.07 | 9.08 |
|
按照生产标准,产品等级规定如下:
尺寸(单位: | 产品等次 |
| 特等品 |
| 优等品 |
| 合格品 |
| 非合格品 |
注:在统计优等品个数时,将特等品计算在内;在统计合格个数时,将优等品(含特等品)算在内,
(1)已知此次抽检的合格率为![]() ,请判断编号为15的产品是否为合格品,并说明理由;
,请判断编号为15的产品是否为合格品,并说明理由;
(2)已知此次及抽检出的优等品尺寸的中位数为![]() .
.
①![]() __________;
__________;
②将这些优等品分成两组,一组尺寸大于![]() ,另一种尺寸不大于
,另一种尺寸不大于![]() ,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.
,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.