题目内容
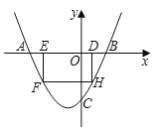
【题目】如图,二次函数![]() 与x轴交于A、B两点,与y轴交于点C,点D与点C关于x轴对称,点P从A点出发向点D运动,点Q在DB上,且∠PCQ=45°,则封闭图形DPCQ(阴影部分)面积的变化情况是( )
与x轴交于A、B两点,与y轴交于点C,点D与点C关于x轴对称,点P从A点出发向点D运动,点Q在DB上,且∠PCQ=45°,则封闭图形DPCQ(阴影部分)面积的变化情况是( )
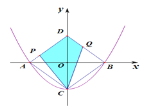
A.一直变大B.始终不变C.先增大后减少D.先减少后增大
【答案】C
【解析】
先证明四边形ABCD是正方形,将△ACP绕点C旋转90°,得到△CAP≌△CBP’进而证得△CPQ≌△CP’Q,得到PQ=PQ’,CB=CH=CA,故△CHP≌△CAP,△CHQ≌△CBQ,得到PH=PA,QH=QB,故S四边形CPDQ=S正方形ABCD-S△CAP-S△CBQ=S正方形ABCD-S△CQP’,当点P是AD中点时,PQ最短,当QP’最短时,△CQP’的面积最小,此时四边形CPDQ的面积最大,故可得到四边形CPDQ的面积先增大后减小.
如图,令![]() =0,解得x1=-2,x2=2,
=0,解得x1=-2,x2=2,
∴A(-2,0), B(2,0),
令x=0,解得y=-2
∴C(0,-2)
故D(0,2)
∴AO=BO=CO=DO,AB⊥CD
则四边形ABCD是正方形,
将△ACP绕点C旋转90°,过C点作CH⊥QP于H点,
∴△CAP≌△CBP’
∴∠PCP’=∠PCB+∠BCP’=∠PCB+∠ACP =90°
∵∠PCQ=45°,
∴∠P’CQ=45°,又CQ=CQ,CP=CP’
∴△CPQ≌△CP’Q
∴PQ=PQ’,
∵CH⊥PQ,CB⊥QP’
∴CB=CH=CA,
又CP=CP
∴△CHP≌△CAP(HL),△CHQ≌△CBQ(HL),
∴PH=PA,QH=QB
故S四边形CPDQ=S正方形ABCD-S△CAP-S△CBQ=S正方形ABCD-S△CQP’
当点P是AD中点时,PQ最短,即QP’最短时,△CQP’的面积最小,
此时四边形CPDQ的面积最大,
故可得到四边形CPDQ的面积先增大后减小.
故选C.