题目内容
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论是___________.
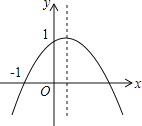
【答案】①③④
【解析】由抛物线的对称轴在y轴右侧,可以判定a、b异号,由此确定①正确;由抛物线与x轴有两个交点得到b2-4ac>0,又抛物线过点(0,1),得出c=1,由此判定②错误;由抛物线过点(-1,0),得出a-b+c=0,即a=b-1,由a<0得出b<1;由a<0,及ab<0,得出b>0,由此判定④正确;由a-b+c=0,及b>0得出a+b+c=2b>0;由b<1,c=1,a<0,得出a+b+c<a+1+1<2,由此判定③正确;由图象可知,当自变量x的取值范围在一元二次方程ax2+bx+c=0的两个根之间时,函数值y>0,由此判定⑤错误.
∵二次函数y=ax2+bx+c(a≠0)过点(0,1)和(-1,0), ∴c=1,a-b+c=0.
①∵抛物线的对称轴在y轴右侧,∴x=-![]() >0, ∴a与b异号,∴ab<0,正确;
>0, ∴a与b异号,∴ab<0,正确;
②∵抛物线与x轴有两个不同的交点,∴b2-4ac>0, ∵c=1,∴b2-4a>0,b2>4a,错误;
④∵抛物线开口向下,∴a<0,∵ab<0,∴b>0.∵a-b+c=0,c=1,∴a=b-1,
∵a<0,∴b-1<0,b<1,∴0<b<1,正确;
③∵a-b+c=0,∴a+c=b,∴a+b+c=2b>0.∵b<1,c=1,a<0,
∴a+b+c=a+b+1<a+1+1=a+2<0+2=2, ∴0<a+b+c<2,正确;
⑤抛物线y=ax2+bx+c与x轴的一个交点为(-1,0),设另一个交点为(x0,0),则x0>0,
由图可知,当x0>x>-1时,y>0,错误; 综上所述,正确的结论有①③④.

【题目】二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)中的x与y的部分对应值如下表所示,则下列结论中,正确的个数有( )
x | -7 | -6 | -5 | -4 | -3 | -2 |
y | -27 | -13 | -3 | 3 | 5 | 3 |
①当x<-4时,y<3②当x=1时,y的值为-13;③-2是方程ax2+(b-2)x+c-7=0的一个根;④方程ax2+bx+c=6有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个