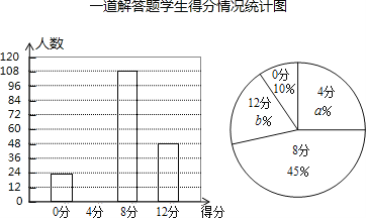
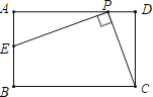
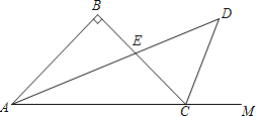
题目内容
【题目】 已知:直线y=-x-4分别交x、y轴于A、C两点,点B为线段AC的中点,抛物线y=ax2+bx经过A、B两点,
(1)求该抛物线的函数关系式;
(2)以点B关于x轴的对称点D为圆心,以OD为半径作⊙D,连结AD、CD,问在抛物线上是否存在点P,使S△ACP=2S△ACD?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,若E为⊙D上一动点(不与A、O重合),连结AE、OE,问在x轴上是否存在点Q,使∠ACQ:∠AEO=2:3?若存在,请求出所有满足条件的点Q的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2+2x;(2)P坐标为(-3-
x2+2x;(2)P坐标为(-3-![]() ,7+
,7+![]() )或(-3+
)或(-3+![]() ,7-
,7-![]() );(3)Q坐标为(4
);(3)Q坐标为(4![]() -8,0)、(-4
-8,0)、(-4![]() -8,0)、(4,0).
-8,0)、(4,0).
【解析】
(1)求直线y=-x-4与坐标轴交点A、C坐标,求AC中点B坐标,即能用待定系数法求抛物线的函数关系式;
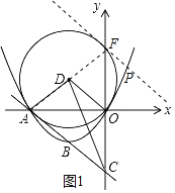
(2)根据点B坐标(-2,-2),可得D坐标为(-2,2),所以△ADO、△ACO均为等腰直角三角形,连接AD并延长交y轴于点F,可知使S△ACP=2S△ACD的点P在过点F且平行于直线y=-x-4的直线上,求出直线与抛物线交点即使所求点P;
(3)由(2)可知,∠AEO度数有两种情况,当点E在优弧AO上时,∠ACQ=![]() ∠AEO=30°.构造直角三角形列方程即可求出Q坐标,当点E在劣弧AO上时,∠AEO=135°,∠ACQ=90°.由等腰直角三角形性质和对称即可求出点Q.
∠AEO=30°.构造直角三角形列方程即可求出Q坐标,当点E在劣弧AO上时,∠AEO=135°,∠ACQ=90°.由等腰直角三角形性质和对称即可求出点Q.
解:(1)∵直线y=-x-4中,y=0时,x=-4;x=0时,y=-4,
∴A(-4,0),C(0,-4),
∵点B为AC中点,
∴B(-2,-2),
∵抛物线y=ax2+bx经过A、B两点,
∴![]() ,
,
解得:![]() ,
,
∴抛物线的函数关系式为y=![]() x2+2x.
x2+2x.
(2)在抛物线上存在点P使S△ACP=2S△ACD.
如图1,连接AD并延长交y轴于点F,
∵y=![]() x2+2x=
x2+2x=![]() (x-2)2-2,
(x-2)2-2,
∴点B为抛物线的顶点,
∵点D为点B关于x轴的对称点,
∴D(-2,2)在抛物线的对称轴上,
∴DA=DO,∠DAO=∠DOA=45°,
∵OA=OC=4,∠AOC=90°,
∴∠OAC=45°,
∴∠DAC=∠DAO+∠OAC=90°,
∴S△ACD=![]() ACAD,
ACAD,
∵∠AOF=90°,
∴AF为⊙D
∴AF=2AD,OF=OA=4即F(0,4),
∵S△ACP=2S△ACD=2![]() ACAD=
ACAD=![]() AC2AD=
AC2AD=![]() ACAF,
ACAF,
∴点P在过点F且平行于直线y=-x-4的直线上,
∴直线PF解析式为y=-x+4,
∵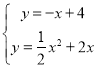 ,
,
解得: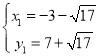 ;
;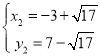 .
.
∴点P坐标为(-3-![]() ,7+
,7+![]() )或(-3+
)或(-3+![]() ,7-
,7-![]() );
);
(3)在x轴上存在点Q使∠ACQ:∠AEO=2:3.
∵∠OAD=∠ODA=45°,
∴∠ADO=90°,
∵点E在⊙D上且不与A、O重合,∠ACQ:∠AEO=2:3.
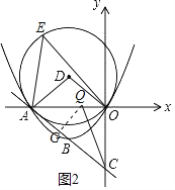
①如图2,当点E在优弧AO上时,∠AEO=![]() ∠ADO=45°,
∠ADO=45°,
∴∠ACQ=![]() ∠AEO=30°,
∠AEO=30°,
过点Q作QG垂直直线AC于点G,设QG=t,
∴Rt△CQG中,CQ=2QG=2t,CG=![]() QG=
QG=![]() t.
t.
∴∠GAQ=∠OAC=45°,
∴Rt△AGQ中,AG=QG=t,AQ=![]() QG=
QG=![]() t.
t.
i)若点Q在线段AO上时,如图2:
则AC=AG+CG=t+![]() t=4
t=4![]() ,
,
解得:t=2![]() -2
-2![]() ,
,
∴AQ=![]() ,
,
∴xQ=-4+4![]() -4=4
-4=4![]() -8;
-8;
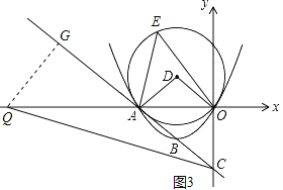
ii)若点Q在线段OA延长上时,如图3:
则AC=CG-AG=![]() t-t=4
t-t=4![]() ,
,
解得:![]() ,
,
∴AQ=![]() ,
,
∴xQ=-4-(4![]() +4)=-4
+4)=-4![]() -8,
-8,
②当点E在劣弧AO上时,∠AEO=![]() (360°-∠ADO)=135°,
(360°-∠ADO)=135°,
∴∠ACQ=![]() ∠AEO=90°.
∠AEO=90°.
∵∠CAO=45°,△ACO是等腰直角三角形,
∴Q点与A点对称,A (-4,0)
∴xQ=4.
综上所述:满足条件的点Q有三个,坐标分别为(4![]() -8,0)、(-4
-8,0)、(-4![]() -8,0)、(4,0)
-8,0)、(4,0)