题目内容
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,连结DB,过点E作EM∥BD,交BA的延长线于点M。
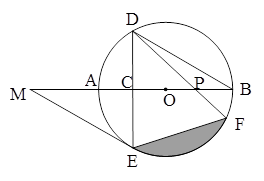
(1)求⊙O的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠DPA=45°时,求图中阴影部分的面积。

(1)求⊙O的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠DPA=45°时,求图中阴影部分的面积。
(1) ;(2)见证明过程:(3)
;(2)见证明过程:(3)
 ;(2)见证明过程:(3)
;(2)见证明过程:(3)

试题分析:
(1)连结OE

∵DE垂直平分OA∴OC=
 ∴
∴ ∴∠COE=60°
∴∠COE=60°∵CE=
 ∴
∴
(2)连结OD
∵AB为直径,AB⊥DE∴
∴∠DOA=∠AOE=60°∴∠B=
 ∵BD∥EM∴∠M=∠B=30°
∵BD∥EM∴∠M=∠B=30°∴∠MEO=90°∴OE⊥ME∴ME是⊙O的切线
(3)连结OF
∵∠DPA=45°∴∠EDP=45°∴∠EOF=2∠EDP=90°
∴

点评:解决本题的关键是圆的概念和性质,把直线与圆相结合是常考点

练习册系列答案
相关题目

 ,求∠APB的度数;
,求∠APB的度数;

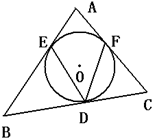
 是
是 的圆心,点
的圆心,点 在
在 ,
, ,则
,则
