题目内容
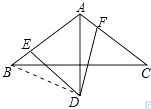
【题目】在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB.∠EDF=60°,其两边分别交边AB,AC于点E,F. 
(1)求证:△ABD是等边三角形;
(2)求证:BE=AF.
【答案】
(1)证明:连接BD,
∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC= ![]() ∠BAC,
∠BAC,
∵∠BAC=120°,
∴∠BAD=∠DAC= ![]() ×120°=60°,
×120°=60°,
∵AD=AB,
∴△ABD是等边三角形
(2)证明:∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,BD=AD
∵∠EDF=60°,
∴∠BDE=∠ADF,
在△BDE与△ADF中,
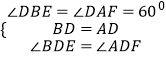 ,
,
∴△BDE≌△ADF(ASA),
∴BE=AF.
【解析】(1)连接BD由等腰三角形的性质和已知条件得出∠BAD=∠DAC= ![]() ×120°=60°,再由AD=AB,即可得出结论;(2)由△ABD是等边三角形,得出BD=AD,∠ABD=∠ADB=60°,证出∠BDE=∠ADF,由ASA证明△BDE≌△ADF,得出BE=AF.
×120°=60°,再由AD=AB,即可得出结论;(2)由△ABD是等边三角形,得出BD=AD,∠ABD=∠ADB=60°,证出∠BDE=∠ADF,由ASA证明△BDE≌△ADF,得出BE=AF.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目