题目内容
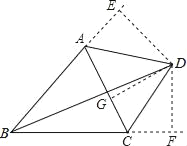
【题目】如图,已知四边形ABCD中,对角线BD平分∠ABC,∠ADB=32°,∠BCD+∠DCA=180°,那么∠ACD为_____度.
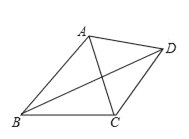
【答案】58.
【解析】
延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,根据BD是∠ABC的平分线可得出DE=DF,过D点作DG⊥AC于G点,进而得出CD为∠ACF的平分线,设∠ABD=x°,则∠ABC=2x°,∠EAD=∠ABD+∠ADB=x°+32°,再根据∠BAE+∠BCF=360°,即可得出结论.
延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,过D点作DG⊥AC于G点,
∵BD是∠ABC的平分线,
∴DE=DF,
又∵∠BCD+∠DCA=180°,
∠BCD+∠DCF=180°,
∴∠ACD=∠DCF,
∴DG=DF=DE
∴AD为∠EAC的平分线,
设∠ABD=x°,则∠ABC=2x°,∠EAD=∠ABD+∠ADB=x°+32°,
∵∠BAE+∠BCF=360°,
∴2(x°+32°)+∠BAC+∠ACB+2∠ACD=360°,
2x°+64°+180°﹣2x°+2∠ACD=360°,
∠ACD=58°.
故答案为:58.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目