题目内容
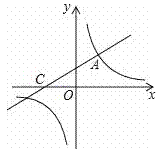
【题目】小红驾车从甲地到乙地．设她出发第x h时距离乙地y km，图中的折线表示她在整个驾车过程中y与x之间的函数关系．
（1）①已知小丽驾车中途休息了1小时，则B点的坐标为（_______，______）；
②求线段AB所表示的y与x之间的函数关系式；
（2）从图象上看，线段AB比线段CD“陡”，请说明它表示的实际意义．
【答案】（1）①3， 100，②
；（2）从甲地到乙地前300米小红驾车的速度比最后100米的速度快.
【解析】试题分析：（1）①由图象可知C点坐标，根据小红驾车中途休息了1小时可得B点坐标；
②利用待定系数法，由A、B两点坐标可求出函数关系式；
（2）根据图形求出从A到B的路程，从C到D的路程，线段AB比线段CD“陡”，说明从甲地到乙地前300米小红驾车的平均速度比最后100米的平均速度快．
试题解析：（1）①由图象可知，C（4，100），
∵小红驾车中途休息了1小时，
∴点B的坐标为（3，100），
故答案为：3，100；
②设y与x之间的函数表达式为y=kx+b，
根据题意，当x=0时，y=400；当x=3时，y=100，
∴
，解得：
，
∴y与x之间的函数表达式：y=-100x+400；
（2）从A到B所对应的路程为300米，从C到D所对应的路程为100米，从图象上看，线段AB比线段CD“陡”，说明从甲地到乙地前300米小红驾车的速度比最后100米的速度快．
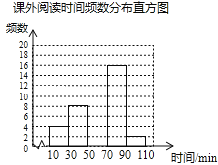
【题目】某学校为了解学生的课外阅读情况，随机抽取了50名学生，并统计他们平均每天的课外阅读时间t（单位：min），然后利用所得数据绘制成如下不完整的统计表．
课外阅读时间t | 频数 | 百分比 |
10≤t＜30 | 4 | 8% |
30≤t＜50 | 8 | 16% |
50≤t＜70 | a | 40% |
70≤t＜90 | 16 | b |
90≤t＜110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题：
（1）a= ，b= ；
（2）将频数分布直方图补充完整；
（3）若全校有900名学生，估计该校有多少学生平均每天的课外阅读时间不少于50min？
