题目内容
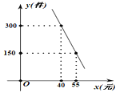
【题目】某网店专门销售某种品牌的学习用品，成本为30元/件，每天销售y（件）与销售单价x（元）之间存在一次函数关系，如图所示．
(1) 求y与x之间的函数关系式；
(2) 当销售单价x为多少元时，每天获取的利润最大，最大利润是多少？
【答案】（1）y=﹣10x+700；（2）当销售单价为50元时，每天获取的利润最大，最大利润是4000元
【解析】
（1）可用待定系数法来确定y与x之间的函数关系式；
（2）利用利润w=销量乘以每件利润进而得出关系式求出答案；
（1）由题意得：
，
解得：
．
故y与x之间的函数关系式为：y=﹣10x+700，
（2）设利润为w=（x﹣30）y=（x﹣30）（﹣10x+700），
w=﹣10x2+1000x﹣21000=﹣10（x﹣50）2+4000，
∵﹣10＜0，∴x=50时，w大=﹣10（50﹣50）2+4000=4000
答：当销售单价为50元时，每天获取的利润最大，最大利润是4000元
练习册系列答案
相关题目
