题目内容
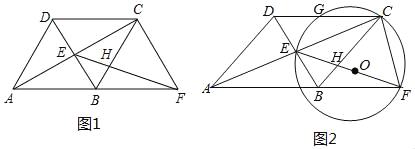
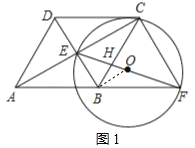
【题目】已知四边形ABCD是边长为10的菱形,对角线AC、BD相交于点E,过点C作CF∥DB交AB延长线于点F,联结EF交BC于点H.
(1)如图1,当EF⊥BC时,求AE的长;
(2)如图2,以EF为直径作⊙O,⊙O经过点C交边CD于点G(点C、G不重合),设AE的长为x,EH的长为y;
①求y关于x的函数关系式,并写出定义域;
②联结EG,当△DEG是以DG为腰的等腰三角形时,求AE的长.
【答案】(1)![]() ;(2)①y=
;(2)①y=![]() (
(![]() <x<10);②
<x<10);②![]() 或
或![]() .
.
【解析】
(1)由菱形性质知DC∥AB、AB=DC、DB和AC互相垂直平分,证平行四边形DBFC得BF=DC=AB=10及∠CAB=∠BCA,由EF⊥BC知∠CAB=∠BCA=∠CFE,据此知△AFC∽△FEC,从而得出FC2=CEAC,即FC2=2AE2,据此可得答案;
(2)①连接OB,由AB=BF、OE=OF知OB∥AC、OB=![]() AE=
AE=![]() EC=
EC=![]() x,据此得
x,据此得![]() =
=![]() =
=![]() 及EH=
及EH=![]() EO,根据EO2=BE2+OB2=-
EO,根据EO2=BE2+OB2=-![]() x2+100可得答案;②分GD=GE和DE=DG两种情况分别求解可得.
x2+100可得答案;②分GD=GE和DE=DG两种情况分别求解可得.
(1)∵四边形ABCD是菱形,
∴DC∥AB、AB=DC、DB和AC互相垂直平分,
∵CF∥DB,
∴四边形DBFC是平行四边形,
∴BF=DC=AB=10,
∴∠CAB=∠BCA,
当EF⊥BC时,∠CAB=∠BCA=∠CFE,
∴Rt△AFC∽Rt△FEC,
∴FC2=CEAC,即FC2=2AE2,
Rt△ACF中,CF2+AC2=AF2,2AE2+4AE2=400,
解得:AE=![]() ;
;
(2)①如图,连接OB,
则AB=BF、OE=OF,
∴OB∥AC,且OB=![]() AE=
AE=![]() EC=
EC=![]() x,
x,
∴![]() =
=![]() =
=![]() ,
,
∴EH=![]() EO,
EO,
在Rt△EBO中,EO2=BE2+OB2=(![]() )2+(
)2+(![]() x)2=﹣
x)2=﹣![]() x2+100,
x2+100,
∴y=![]() EO=
EO=![]() (
(![]() <x<10);
<x<10);
②当GD=GE时,有∠GDE=∠GED,
∵AC⊥DB,∠DEC=90°,
∴∠GCE=∠GEC,
∴GE=GC,
∴GD=GC,即G为DC的中点,
又∵EO=FO,
∴GO是梯形EFCD的中位线,
∴GO=![]() =
=![]() DE,
DE,
∴![]() y=
y=![]() ,
,
∴![]() =
=![]() ,
,
解得:x=![]() ;
;
如图2,当DE=DG时,连接OD、OC、GO,
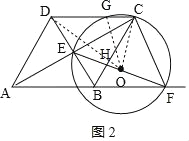
在△GDO和△EDO中,
∵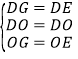 ,
,
∴△GDO≌△EDO(SSS),
∴∠DEO=∠DGO,
∴∠CGO=∠BEO=∠OFC,
∴∠CGO=∠OCG=∠OFC=∠OCF,
∴GC=CF,
∴DC=DG+GC=DE+2DE=10,
即3![]() =10,
=10,
解得:x=![]() ,
,
综上,AE的长为![]() 或
或![]() .
.

【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.