题目内容
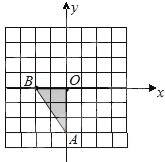
【题目】如图,在平面直角坐标系中,已知△AOB,A(0,﹣3),B(﹣2,0).将△OAB先绕点B 逆时针旋转90°得到△BO1A1,再把所得三角形向上平移2个单位得到△B1A2O2;
(1)在图中画出上述变换的图形,并涂黑;
(2)求△OAB在上述变换过程所扫过的面积.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据旋转的性质,结合网格结构找出点A、O的对应点A1、O1,再与点B顺次连接即可得到△BO1A1;再根据平移的性质,结合网格结构找出点B、A1、O1的对应点B1、A2、O2,然后顺次连接即可得解;
(2)结合图形不难看出,变换过程所扫过的面积为扇形BAA1,与梯形A1A2O2B的面积的和,然后根据扇形的面积公式与梯形的面积公式列式进行计算即可求解.
(1)如图所示;
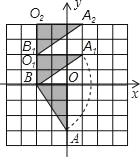
(2)在Rt△AOB中,AB=![]() ,
,
∴扇形BAA1的面积=![]() ,
,
梯形A1A2O2B的面积=![]() ×(2+4)×3=9,
×(2+4)×3=9,
∴变换过程所扫过的面积=扇形BAA1的面积+梯形A1A2O2B的面积=![]() +9.
+9.

练习册系列答案
相关题目