题目内容
【题目】探索函数![]() 的图象和性质.
的图象和性质.
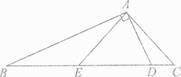
已知函数y=x(x>0)和![]() 的图象如图所示,若P为函数
的图象如图所示,若P为函数![]() 图象上的点,过P作PC垂直于x轴且与直线、双曲线、x轴分别交于点A、B、C,则PC=
图象上的点,过P作PC垂直于x轴且与直线、双曲线、x轴分别交于点A、B、C,则PC= ![]() =AC+BC,从而“点P可以看作点A的沿竖直方向向上平移BC个长度单位(PA=BC)而得到”.
=AC+BC,从而“点P可以看作点A的沿竖直方向向上平移BC个长度单位(PA=BC)而得到”.
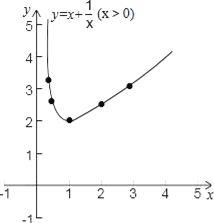
(1)根据以上结论,请在下图中作出函数![]() 图象上的一些点,并画出该函数的图象.
图象上的一些点,并画出该函数的图象.
(2)观察图象,写出函数![]() 两条不同类型的性质.
两条不同类型的性质.

【答案】(1)图象见解析;(2)函数两条不同类型的性质是:当0<x<1时,y 随x的增大而减小,当x>1时,y 随x的增大而增大;当x=1时,函数y=x+![]() (x>0)的最小值是2.
(x>0)的最小值是2.
【解析】试题分析:(1)利用已知函数解析式,进而求出图象上点的坐标,进而求出在图象中画出即可即可;
(2)利用函数图象得出函数性质即可.
试题解析:(1)如图所示:
x |
|
| 1 | 2 | 3 |
y | 3 | 2 | 2 | 2 | 3 |
(2)函数两条不同类型的性质是:
当0<x<1时,y 随x的增大而减小,当x>1时,y 随x的增大而增大;
当x=1时,函数y=x+![]() (x>0)的最小值是2.
(x>0)的最小值是2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目