题目内容
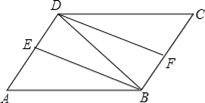
【题目】如图,点D是等边△ABC中BC边上一点,过点D分别作DE∥AB,DF∥AC,交AC,AB于E,F,连接BE,CF,分别交DF,DE于点N,M,连接MN.试判断△DMN的形状,并说明理由.
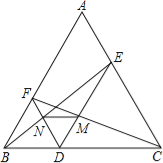
【答案】△DMN为等边三角形,理由见解析.
【解析】试题分析:由已知可得△BDF、△EDC是等边三角形,从而可证△BDE≌△FDC,继而可证△NDE≌△MDC,从而问题得以解决.
试题解析:△DMN为等边三角形,理由如下:
∵△ABC为等边三角形,∴∠ACB=∠ABC=60°,∵DE//AB,DF∥AC,∴∠EDC=∠ABC=60°,∠FDB=∠ACB=60°,∴∠FDE=60°,△BDF、△EDC是等边三角形,∴BD=FD,ED=CD,∵∠BDE=∠FDC=120°,∴△BDE≌△FDC,∴∠BED=∠FCD,又∵∠NDE=∠MDC=60°,∴△NDE≌△MDC,∴DN=DM,∴△DMN是等边三角形.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目