��Ŀ����
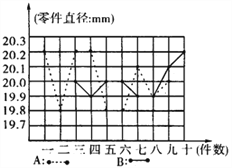
����Ŀ��Ϊѡ��һ��ѧ���μ�ȫ��ʵ������ܾ�����A��B��λͬѧ��Уʵϰ�����ֳ����мӹ�ֱ��Ϊ20mm������IJ��ԣ������ӹ���10����������������������ͼ����ʾ����λ��mm����
���ݲ��Եõ����й����ݣ��Խ���������⣺
ƽ���� | ���� | ��ȫ����Ҫ��ĸ��� | |
A | 20 | 0.026 | 2 |
B | 20 | S2B | 5 |
��1������ƽ��������ȫ����Ҫ��ĸ���������Ϊ________�ijɼ���Щ��
��2�������S2B�Ĵ�С������ƽ�����뷽�˵��˭�ijɼ���Щ��
��3������ͼ���������Ƽ������мӹ��������ԶԶ����10����ʵ�����������Ϊ��˭ȥ�����Ϻ��ʣ�˵��������ɣ�
���𰸡���1��B����2��B�ijɼ���Щ����3�����ɺ������ɣ���������
�������������������1������A��B��λͬѧ�ɼ���ƽ������ͬ������ȫ����Ҫ��ĸ���Bͬѧ�϶࣬����Bͬѧ�ijɼ���Щ��
��2�����÷�����㹫ʽ�������SB2�Ĵ�С��Ȼ�����÷����ƽ���������弴����⣻
��3�����ã�1����2���Ľ��۽��ʵ�����˵�����⼴�ɽ�����⣮
���������
��1������A��B��λͬѧ�ɼ���ƽ������ͬ������ȫ����Ҫ��ĸ���Bͬѧ�϶࣬����Bͬѧ�ijɼ���Щ��
��2����SB2��![]() [4(20.020.0)2+3(19.920.0)2+(20.120.0)2+(19.9520.0)2+(20.220.0)2]
[4(20.020.0)2+3(19.920.0)2+(20.120.0)2+(19.9520.0)2+(20.220.0)2]
=0.008��
�֡�SA2=0.026��
����SA2��SB2��
��ƽ������ͬ������£�B�IJ���С������B�ijɼ���Щ��
��3����ͼ�е��������ƿ�֪��A�ijɼ�ǰ������ϴ����ϴ�B�ijɼ��Ƚ��ȶ�������Ԥ��B��DZ����ѡ��Bȥ������
[˵������3���Ĵ𰸲�Ψһ��ֻҪ����ͳ��֪ʶ��Ϊ�������ݼ��ɣ���ֻ�ش�ѡA��ѡB��û����ͳ��֪ʶ��Ϊ�������ݵIJ��÷�]

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ���Ķ����в��ϣ�
Ϊ���ڼס�������ѧ����ѡ��һ�˲μ���ѧ����������ͬ�����£������ǽ�����10�β��飬�ɼ����£�����λ���֣�
�׳ɼ� | 76 | 84 | 90 | 86 | 81 | 87 | 86 | 82 | 85 | 83 |
�ҳɼ� | 82 | 84 | 85 | 89 | 79 | 80 | 91 | 89 | 74 | 79 |
�ش��������⣺
��1����ѧ���ɼ���������_______���֣�����ѧ���ɼ�����λ����_______���֣���
��2������ѧ���ɼ���ƽ������![]() ������ѧ���ɼ���ƽ������
������ѧ���ɼ���ƽ������![]() ������
������![]() ����
����![]() ���Ĵ�С��ϵ�ǣ�________��
���Ĵ�С��ϵ�ǣ�________��
��3��������֪��S2��=13.2��S2��=26.36�������____________���ü������������Ա�����
��4�������������85�֣���85�֣�����Ϊ���㣬���������Ϊ________���ҵ�������Ϊ________��
����Ŀ��ij��湫˾����Ƹ������Ա1������A��B��C������ѡ�˽����������ʲ��ԣ����ǵĸ�����Գɼ����±���ʾ��
������Ŀ | ���Գɼ�/�� | ||
A | B | C | |
רҵ֪ʶ | 54 | 72 | 81 |
�������� | 69 | 81 | 57 |
�������� | 90 | 60 | 81 |
��1�������������Ե�ƽ���ɼ�ȷ��Ƹ����Ա����ô˭��Ƹ�ã�
��2������ʵ����Ҫ����˾��רҵ֪ʶ������������������������Եĵ÷ְ�3��5��2�ı�ȷ�����˵IJ��Գɼ�����ʱ˭����Ƹ�ã�



