题目内容
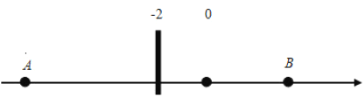
【题目】数轴上任意两点之间的距离均可用“右﹣左”表示，即右边的数（较大）减去左边的数（较小）．已知数轴上两点A、B对应的数分别为﹣2、5，则A、B两点之间的距离记为AB，且AB＝5﹣（﹣2）＝7．P为数轴上的动点，其对应的数为x．
（1）若点P到A，B两点的距离相等，写出点P对应的数；
（2）数轴上是否存在点P，使点P到A，B两点的距离之和为11，若存在，请求出x的值；若不存在，请说明理由；
（3）若点P在原点，现在A，B，P三个点均向左匀速运动，其中点P的速度为每秒1个单位；A，B两点中有一个点速度与点P的速度一致，另一个点以每秒3单位的速度运动；则几秒后点P到A，B两点的距离相等？
【答案】（1）点P对应的数为1.5；（2）x＝7或﹣4；（3）①当点A与点P的运动速度相等时，
秒或
秒后点P到A，B两点的距离相等；②当点B与点P的运动速度相等时，秒后点P到A，B两点的距离相等．
【解析】
（1）根据P点表示的数为x，利用距离相等列出方程解答即可；
（2）分当P在AB之间（包括与A，B重合）时，当P点在A点的左边时，当P点在B点的右边时，根据P点到A，B两点的距离和为11列出方程解答即可；
（3）设出运动时间，分情况讨论：①当点A与点P的运动速度相等时；②当点B与点P的运动速度相等时，分别根据两点之间的距离求法表示出PA和PB，结合PA＝PB列出方程求解即可.
解：（1）由题意得x﹣（﹣2）＝5﹣x，
解得x＝1.5，
即点P对应的数为1.5；
（2）①当P在AB之间（包括与A，B重合）时，
PA+PB＝x﹣（﹣2）+5﹣x＝7，不符合要求，
②当P在B的右边时，PA+PB＝x﹣（﹣2）+x﹣5＝2x﹣3，
令2x﹣3＝11，
解得x＝7，
③当P在A的左边时，PA+PB＝﹣2﹣x+5﹣x＝3﹣2x，
令3﹣2x＝11，
解得x＝﹣4，
综上所述，x＝7或﹣4；
（3）设运动时间为t秒，
由题意可知：A、B对应的数分别为﹣2、5，P对应的数为0，
①当点A与点P的运动速度相等时，t秒后A点表示的数为－2－t，P点表示的数为－t，B点表示的数为5－3t，
则PA＝－t－（－2－t）＝2，PB＝
，
由点P到A，B两点的距离相等得：
，
解得：t＝或；
②当点B与点P的运动速度相等时，t秒后A点表示的数为－2－3t，P点表示的数为－t，B点表示的数为5－t，
则PA＝－t－（－2－3t）＝2+2t，PB＝5－t－（－t）＝5，
由点P到A，B两点的距离相等得：5＝2+2t，
解得t＝，
综上所述：当点A与点P的运动速度相等时，秒或秒后点P到A，B两点的距离相等；当点B与点P的运动速度相等时，秒后点P到A，B两点的距离相等．
