��Ŀ����
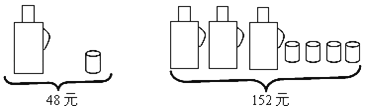
����Ŀ�������̻����ž����������еIJ�ͬ����ܴ��������ͣ��ڷ��ڳ�����Ҫ�����������A��B���������;����õ��ž黨��A������ÿ�����öž黨25�裬B������ÿ�����öž黨35�裬����������⣺
��1����֪��������������A��B����������60����ǡ������1700��ž黨��A��B���������������˶��ٸ���
��2���������һ��A�����͵ijɱ�W��������![]() �Ĺ�ϵʽΪ��W��100�D
�Ĺ�ϵʽΪ��W��100�D![]() x ��0��x��50��������һ��B�����͵ijɱ�Ϊ80Ԫ�����ڹۺ��������Ҳ�����A��B����������50����Ҫ��ÿ�������Ͳ�������20�������ҳɱ��ܶ�y��Ԫ��������4500Ԫ����. ����Ҫ���ܷ�ͬʱ���㣿����ͨ������˵������.
x ��0��x��50��������һ��B�����͵ijɱ�Ϊ80Ԫ�����ڹۺ��������Ҳ�����A��B����������50����Ҫ��ÿ�������Ͳ�������20�������ҳɱ��ܶ�y��Ԫ��������4500Ԫ����. ����Ҫ���ܷ�ͬʱ���㣿����ͨ������˵������.
���𰸡�(1) A�������ʹ�����40����B�������ʹ�����20��;(2) ��![]() ʱ�������ֵΪ
ʱ�������ֵΪ![]() ,4500��������ͬʱ��������Ҫ��.
,4500��������ͬʱ��������Ҫ��.
��������������(1)����A�������ʹ�����x������B�������ʹ����ˣ�60��x���������������г����̴Ӷ��ó�x��ֵ��(2)����A�������ʹ�����x������B�������ʹ����ˣ�50��x��������������ó�y��x�ĺ�����ϵʽ���ó����ֵ���Ӷ������ж��Ƿ���ȷ��
��⣺��1����A�������ʹ�����x������B�������ʹ����ˣ�60��x������
25x+35��60��x��=1700�� ��ã�x=40��60��x=20��
��A�������ʹ�����40����B�������ʹ�����20����
��2����ͬʱ��������Ҫ��
���ɣ���A�������ʹ�����x������B�������ʹ����ˣ�50��x������
�ɱ��ܶ�y��A������������x�ĺ�����ϵʽΪ��y=x��100��![]() ��+80��50��x��=��
��+80��50��x��=��![]() +20x+4000=
+20x+4000=![]() ��
��
��x��20��50��x��20�� ��20��x��30�� �൱x=20ʱ��yȡ�����ֵ����ʱy=4200��
��4200��4500�� ����ͬʱ��������Ҫ��

����Ŀ��ij���г���һ�ܼƻ�����150�����г���ƽ��ÿ�������������ڸ���ԭ��ʵ��ÿ����������ƻ�������г��룬�±���ij�ܵ��������������Ϊ��������Ϊ������
���� | һ | �� | �� | �� | �� | �� | �� |
���� |
|
|
|
|
|
|
|
��1�����ݼ�¼��֪ǰ���칲���� ����
��2����������һ������������ٵ�һ������� ����
��3���ó�ʵ�мƻ������ƣ�ÿ����![]() Ԫ�������������ÿ����
Ԫ�������������ÿ����![]() Ԫ��������һ����
Ԫ��������һ����![]() Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ��٣�
Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ��٣�