题目内容
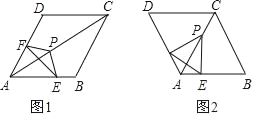
【题目】如图,E是正方形ABCD外一点,且DE=CE=![]() ,连接AE.
,连接AE.
(1)将△ADE绕点D逆时针旋转90°,作出旋转后的图形.
(2)如果∠AED=15°,判断△DEC的形状,并说明理由.

【答案】(1)见解析(2)△DEC是等边三角
【解析】分析:(1)根据旋转变换的定义和性质即可作图;
(2)先利用旋转性质知△DEF为等腰直角三角形,继而得出∠CFE=30°、∠AEF=60°、∠EGF=90°,从而求得EF=2、GE=1、CG=GE,据此知∠CEG=45°,根据∠CED=∠CEG+∠AED=60°、CE=DE即可得证.
详解:(1)如图所示,△CDF即为所求;

(2)△DEC是等边三角形,
理由:如图,连接EF,记AE、CF的交点为G,
由(1)可得DF=DE、∠EDF=90°、∠CFD=∠AED=15°,
∴∠DFE=∠DEF=45°,
∴∠CFE=∠DFE﹣∠CFD=30°,∠AEF=∠AED+∠DEF=60°,
∴∠EGF=90°,
∴GE=![]() EF,
EF,
∵EF=![]() =2,
=2,
∴GE=1,
∴CG=![]() =1,
=1,
∴CG=EG,
∵∠CGE=90°,
∴∠CEG=45°,
∴∠CED=∠CEG+∠AED=60°,
∵CE=DE,
∴△DEC为等边三角形.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目