题目内容
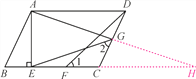
【题目】如图,在ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.

(1)若CF=2,AE=3,求BE的长;
(2)求证:∠CEG=![]() ∠AGE.
∠AGE.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】试题分析:(1)求出DC=CE=2CF=4,求出AB,根据勾股定理求出BE即可;
(2)延长AG,BC交于点H,证△CEG≌△CDF,推出CG=CF,求出M为AE中点,得出等腰三角形AGE,根据性质得出GM是∠AGE的角平分线,即可得出答案.
试题解析:(1)∵点F为CE的中点,∴CE=CD=2CF=4.
又∵四边形ABCD为平行四边形,∴AB=CD=4.
在Rt△ABE中,由勾股定理,得BE=![]() =
=![]() .
.
(2)证明:延长AG,BC交于点H.
∵∠2=∠1,∠ECG=∠DCF,CE=CD
∴△CEG≌△CDF(AAS).∴CG=CF.
∵CD=CE=2CF,∴CG=GD.
∵在ABCD中,AD∥BC,
∴∠DAG=∠CHG,∠ADG=∠HCG.
∴△ADG≌△HCG(AAS).∴AG=HG.
∵∠AEH=90°,∴EG=AG=HG.∴∠CEG=∠H.
∵∠AGE=∠CEG+∠H,
∴∠AGE=2∠CEG,即∠CEG=![]() ∠AGE.
∠AGE.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案【题目】某市在城中村改造中,需要种植A、B两种不同的树苗共3000棵,经招标,承包商以15万元的报价中标承包了这项工程,根据调查及相关资料表明,A、B两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
A | 28 | 90% |
B | 40 | 95% |
设种植A种树苗x棵,承包商获得的利润为y元.
(1)求y与x之间的函数关系式;
(2)政府要求栽植这批树苗的成活率不低于93%,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
(3)在达到(2)中政府的要求并获得最大利润的前提下,承包商用绿化队的40人种植这两种树苗,已知每人每天可种植A种树苗6棵或B种树苗3棵,如何分配人数才能使种植A、B两种树苗同时完工.