题目内容
【题目】如图,在△ABC中,∠ACB=90,∠ABC=45 ,点O是AB的中点,过A、C两点向经过点O的直线作垂线,垂足分别为E、F.
(1)如图①,求证:EF=AE+CF.
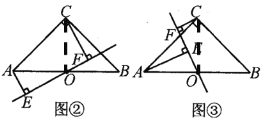
(2)如图②,图③,线段EF、AE、CF之间又有怎样的数量关系?请直接写出你的猜想.
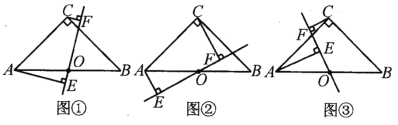
【答案】(1)见解析;(2)图②:EF=AE+CF 图③:EF=AE-CF,见解析
【解析】
(1)连接OC,运用AAS证△AOE≌△OCF即可;
(2)按(1)中的方法,连接OC,证明△AOE≌△OCF,即可得出结论
(1)连接OC,∵△ABC是等腰直角三角形,
∴∠AOC=90°,AO=CO,
∵∠AOE+∠COF=90°,∠EAO+∠AOE=90°,
∴∠EAO=∠COF,
又∵AO=CO,∠AEO=∠CFO,
∴△AOE≌△OCF(AAS)
∴OE=CF,AE=OF ∴EF=AE+CF
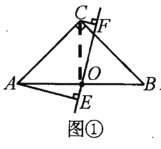
(2)如图②,连接OC,
∵△ABC是等腰直角三角形,
∴∠AOC=90°,AO=CO,
∵∠AOE+∠COF=90°,∠EAO+∠AOE=90°,
∴∠EAO=∠COF,
又∵AO=CO,∠AEO=∠CFO,
∴△AOE≌△OCF(AAS)
∴OE=CF,AE=OF
∴EF=AE+CF.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目