题目内容
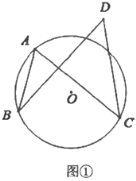
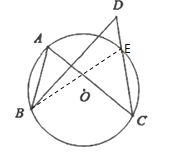
【题目】（1）如图①，点
，
，
在
上，点
在外，比较
与
的大小，并说明理由；
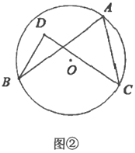
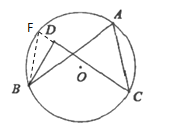
（2）如图②，点，，在上，点在内，比较与的大小，并说明理由；
（3）利用上述两题解答获得的经验，解决如下问题：
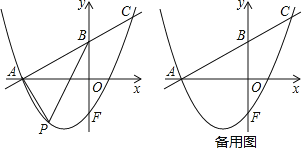
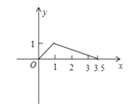
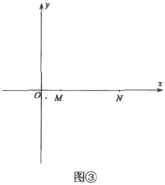
在平面直角坐标系中，如图③，已知点
，
，点
在
轴上，试求当
度数最大时点的坐标.
【答案】（1）
；理由详见解析；（2）
；理由详见解析；（3）
， 
【解析】
（1）根据圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，构建圆周角，然后利用三角形外角性质比较即可；
（2）根据圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，构建圆周角，然后利用三角形外角性质比较即可；
（3）根据圆周角定理，结合（1）（2）的结论首先确定圆心的位置，然后即可得出点P的坐标.
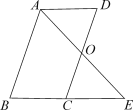
（1）
交
于点
，连接
，如图所示：
中
又
∴
（2）延长交于点
，连接
，如图所示：
中
又
∴
（3）由（1）（2）结论可知，当OP=2.5时，∠MPN最大，如图所示：
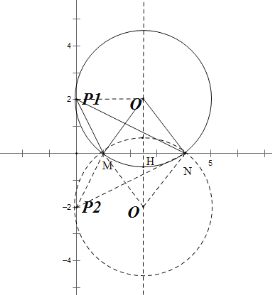
∴OM=2.5，MH=1.5
∴
∴，
练习册系列答案
相关题目
