��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�������y=x2+��k��1��x��k��ֱ��y=kx+1����A��B���㣬��A�ڵ�B����࣮


��1����ͼ1����k=1ʱ��ֱ��д��A��B��������ꣻ
��2���ڣ�1���������£���PΪ�������ϵ�һ�����㣬����ֱ��AB�·����������ABP��������ֵ����ʱ��P�����ꣻ
��3����ͼ2��������y=x2+��k��1��x��k��k��0����x�ύ�ڵ�C��D���㣨��C�ڵ�D����ࣩ����ֱ��y=kx+1���Ƿ����Ψһһ��Q��ʹ����OQC=90���������ڣ��������ʱk��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��A(-1,0) ��B(2,3)
��2����ABP������s=![]() ; P��
; P��![]() ,-
,-![]() ��
��
��3�����ڣ�k=![]()
��������
���⣨1�� ��k=1ʱ�������߽���ʽΪy=x2��1��ֱ�߽���ʽΪy=x+1��Ȼ��ⷽ����![]() ���ɣ�
���ɣ�
��2�� ��P��x��x2��1��������P��PF��y�ᣬ��ֱ��AB�ڵ�F����F��x��x+1������������S��ABP=S��PFA+S��PFB��
���ú�x�Ĵ���ʽ��ʾΪS��ABP=��x2+x+2���䷽���ù�ʽȷ���������꼴�ɣ���3�� ��ֱ��AB��y=kx+1��x�ᡢy��ֱ��ڵ�E��F����k�ֱ��ʾ��E�����꣬��F�����꣬�Լ���C�����꣬Ȼ����Rt��EOF�У��ɹ��ɶ�����ʾ��EF�ij����������Ψһһ��Q��ʹ����OQC=90��������OCΪֱ����Բ��ֱ��AB�����ڵ�Q�����NΪOC�е㣬����NQ����������֤����EQN�ס�EOF��Ȼ��������ʶ�Ӧ�߳ɱ������ɵù���k�ķ��̣��ⷽ�̼���.
����������⣺��1����k=1ʱ�������߽���ʽΪy=x2��1��ֱ�߽���ʽΪy=x+1��
������������ʽ���ã�x2��1=x+1��
��ã�x=��1��x=2��
��x=��1ʱ��y=x+1=0����x=2ʱ��y=x+1=3��
��A����1��0����B��2��3���� 4��
��2����P��x��x2��1����
���ͼ2��ʾ������P��PF��y�ᣬ��ֱ��AB�ڵ�F����F��x��x+1����
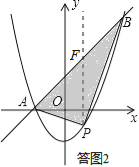
��PF=yF��yP=��x+1������x2��1��=��x2+x+2��
S��ABP=S��PFA+S��PFB=PF��xF��xA��+PF��xB��xF��=PF��xB��xA��=PF
��S��ABP=����x2+x+2��=����x��![]() ��2+
��2+![]()
��x=![]() ʱ��yP=x2��1=��
ʱ��yP=x2��1=��![]() ��
��
���ABP������ֵΪ![]() ����ʱ��P����Ϊ��
����ʱ��P����Ϊ��![]() ����
����![]() ���� 8��
���� 8��
��3����ֱ��AB��y=kx+1��x�ᡢy��ֱ��ڵ�E��F��
��E����![]() ��0����F��0��1����OE=
��0����F��0��1����OE=![]() ��OF=1��
��OF=1��
��Rt��EOF�У��ɹ��ɶ����ã�EF=![]() =
=![]() ��
��
��y=x2+��k��1��x��k=0������x+k����x��1��=0����ã�x=��k��x=1��
��C����k��0����OC=k��
�������Ψһһ��Q��ʹ����OQC=90�������ͼ3��ʾ��
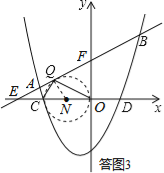
����OCΪֱ����Բ��ֱ��AB�����ڵ�Q������Բ�ܽǶ�������ʱ��OQC=90����
���NΪOC�е㣬����NQ����NQ��EF��NQ=CN=ON=![]() ��
��
��EN=OE��ON=![]() ��
��![]() ��
��
�ߡ�NEQ=��FEO����EQN=��EOF=90����
���EQN�ס�EOF��
��![]() ������
������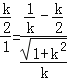 ��
��
��ã�k=��![]() ��
��
��k��0��
��k=![]() ��
��
������Ψһһ��Q��ʹ����OQC=90������ʱk=![]() �� 12��
�� 12��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�



