题目内容
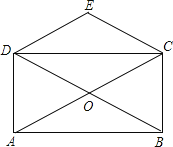
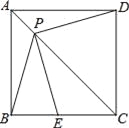
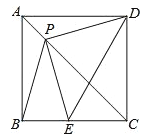
【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
【答案】(1)见解析(2)∠PED=45°.
【解析】试题(1)根据正方形的性质四条边都相等可得BC=CD,对角线平分一组对角线可得∠ACB=∠ACD,然后利用“边角边”证明△PBC和△PDC全等,根据全等三角形对应边相等可得PB=PD,然后等量代换即可得证;(2)根据全等三角形对应角相等可得∠PBC=∠PDC,根据等边对等角可得∠PBC=∠PEB,从而得到∠PDC=∠PEB,再根据∠PEB+∠PEC=180°求出∠PDC+∠PEC=180°,然后根据四边形的内角和定理求出∠DPE=90°,判断出△PDE是等腰直角三角形,根据等腰直角三角形的性质求解即可.
试题解析:(1)∵四边形ABCD是正方形,
∴BC=CD,∠ACB=∠ACD,
在△PBC和△PDC中,
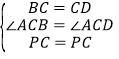 ,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)判断∠PED=45°.
∵四边形ABCD是正方形,
∴∠BCD=90°,
∵△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
在四边形PECD中,∠EPD=360°﹣(∠PDC+∠PEC)﹣∠BCD=360°﹣180°﹣90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴∠PED=45°.

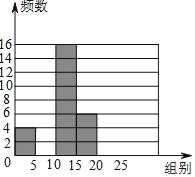
【题目】珠海市某中学开展主题为“我爱阅读”的专题调查活动,为了解学校1200名学生一年内阅读书籍量,随机抽取部分学生进行统计,绘制成如下尚未完成的频数分布表和频数分布直方图.请根据图表,解答下面的问题:
分组 | 频数 | 频率 |
0≤x<5 | 4 | 0.08 |
5≤x<10 | 14 | 0.28 |
10≤x<15 | 16 | a |
15≤x<20 | b | c |
20≤x<25 | 10 | 0.2 |
合计 | d | 1.00 |
(1)a= ,b= c= .
(2)补全频数分布直方图;
(3)根据该样本,估计该校学生阅读书籍数量在15本或15本以上的人数.