题目内容
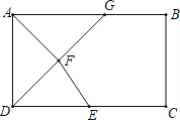
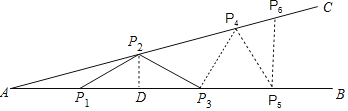
【题目】如图钢架中,∠A=15°,现焊上与AP1等长的钢条P1P2,P2P3…来加固钢架,若最后一根钢条与射线AB的焊接点P到A点的距离为4+2![]() ,则所有钢条的总长为( )
,则所有钢条的总长为( )
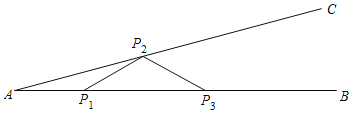
A.16B.15C.12D.10
【答案】D
【解析】
根据已知利用等腰三角形的性质及三角形外角的性质,找出图中存在的规律,求出钢条的根数,然后根据最后一根钢条与射线AB的焊接点P到A点的距离即AP5为4+2![]() ,设AP1=a,作P2D⊥AB于点D,再用含a的式子表示出P1P3,P3P5,从而可求出a的值,即得出每根钢条的长度,从而可以求得所有钢条的总长.
,设AP1=a,作P2D⊥AB于点D,再用含a的式子表示出P1P3,P3P5,从而可求出a的值,即得出每根钢条的长度,从而可以求得所有钢条的总长.
解:如图,∵AP1与各钢条的长度相等,∴∠A=∠P1P2A=15°,
∴∠P2P1P3=30°,∴∠P1P3P2=30°,∴∠P3P2P4=45°,
∴∠P3P4P2=45°,∴∠P4P3P5=60°,∴∠P3P5P4=60°,
∴∠P5P4P6=75°,∴∠P4P6P5=75°,∴∠P6P5B=90°,
此时就不能再往上焊接了,综上所述总共可焊上5根钢条.
设AP1=a,作P2D⊥AB于点D,
∵∠P2P1D=30°,∴P2D=![]() P1P2,∴P1D=
P1P2,∴P1D=![]() a,
a,
∵P1P2=P2P3,∴P1P3=2P1D =![]() a,
a,
∵∠P4P3P5=60°,P3P4=P4P5,∴△P4P3P5是等边三角形,∴P3P5=a,
∵最后一根钢条与射线AB的焊接点P到A点的距离为4+2![]() ,
,
∴AP5=a+![]() a+a=4+2
a+a=4+2![]() ,
,
解得,a=2,
∴所有钢条的总长为2×5=10,
故选:D.

【题目】“文明礼仪”在人们长期生活和交往中逐渐形成,并以风俗、习惯等方式固定下来的.我们作为具有五千年文明史的“礼仪之邦”,更应该用文明的行为举止, 合理的礼仪来待人接物.为促进学生弘扬民族文化、展示民族精神,某学校开展“文明礼仪”演讲比赛,八年级(1)班,八年级(2)班各派出 5 名选手参加比赛,成绩如图所示.
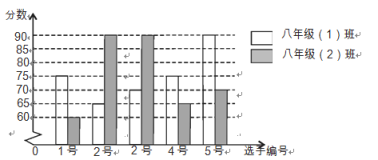
(1)根据图,完成表格:
平均数(分) | 中位数(分) | 极差(分) | 方差 | |
八年级(1)班 | 75 |
| 25 |
|
八年级(2)班 | 75 | 70 |
| 160 |
(2)结合两班选手成绩的平均分和方差,分析两个班级参加比赛选手的成绩;
(3)如果在每班参加比赛的选手中分别选出3人参加决赛,从平均分看,你认为哪个班的实力更强一些? 说明理由.