题目内容
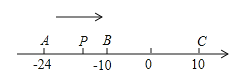
【题目】已知数轴上有A、B、C三个点，分别表示有理数－24，－10，10，动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．
（1）用含t的代数式表示P到点A和点C的距离：PA= ，PC= ．
（2）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，运动到终点A．
①在运动过程中，t为何值时P与Q重合？
②在点Q开始运动后，P、Q两点之间的距离能否为2个单位？如果能，请求出此时点P表示的数；如果不能，请说明理由．
【答案】（1）t，34－t；（2）①21或
；②t为20、22、27、28时，PQ=2．．点P表示的数分别为：4，2，3，4．
【解析】试题分析：（1）数轴上求距离，利用大的(右边)坐标减去小的（左边）坐标，或者任意两个坐标作差再求绝对值. (2)根据题意求解绝对值方程.
试题解析：
解：（1）PA=t，PC=34-t，（2）①21或
②P从A到B需要时间：14秒，QA=3（t14），当Q从A到C过程：PQ=|t3（t14）|=|422t|=2，422t=2得，t=20，422t=2得，t=22，当Q从C往回，Q到达C需要时间： 
， CQ=3（t14
）=3t76，PQ=|34t（3t76）|=|1104t|=2，1104t=±2，t=27或t=28.
答：t为20、22、27、28时，PQ=2.
点P表示的数分别为：4；2；3；4.
练习册系列答案
相关题目
