��Ŀ����
����Ŀ�����壺��ͼ��1�������ֱ��ԡ�ABC������AC��BC��ABΪ���������������������ACDE��BCFG��ABMN�����������������Ϊ��ABC����չ��Ҷ�����Σ�������������������Ϊ��ABC����չ˫Ҷ�����Σ� 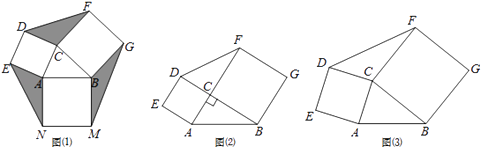
��1������ABC����չ˫Ҷ������ACDE��BCFG���ǡ�ABC����DCF������ֱ�ΪS1��S2 �� ����ͼ��2��������ACB=90��ʱ����֤��S1=S2 ��
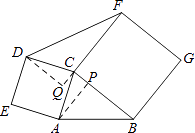
����ͼ��3��������ACB��90��ʱ��S1��S2�Ƿ���Ȼ��ȣ���˵�����ɣ�
��2����֪��ABC�У�AC=3��BC=4��������չ��Ҷ�����Σ��ǡ�DCF����AEN����BGM�������ΪS��������ͼ��1��̽��������ACB�Ķ��������仯ʱ��S��ֵ�Ƿ����仯�������䣬���S��ֵ�����仯�����S�����ֵ��
���𰸡�
��1��֤������ͼ1��
��������ACDE��������BCFG��
��AC=DC��BC=FC����ACD=��BCF=90�㣬
�ߡ�ACB=90�㣬���DCF=90�㣬
���ACB=��DCF=90�㣮
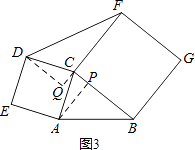
�ڡ�ABC�͡�DFC�У�
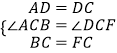 ��
��
���ABC�ա�DFC��SAS����
��S��ABC=S��DFC��
��S1=S2
��S1=S2���������£�
�⣺��ͼ3������A��AP��BC�ڵ�P������D��DQ��FC��FC���ӳ����ڵ�Q��
���APC=��DQC=90�㣮
���ı���ACDE��BCFG��Ϊ�����Σ�
��AC=CD��BC=CF��
�ߡ�ACP+��ACQ=90�㣬��DCQ+��ACQ=90�㣮
���ACP=��DCQ��
�ڡ�APC�͡�DQC��
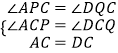 ��
��
���APC�ա�DQC��AAS����
��AP=DQ��
��BC��AP=DQ��FC��
�� ![]() BC��AP=
BC��AP= ![]() DQ��FC
DQ��FC
��S1= ![]() BC��AP��S2=
BC��AP��S2= ![]() FC��DQ��
FC��DQ��
��S1=S2
��2���ɣ�2���ã�S�ǡ�ABC�����������
ҪʹS���ֻ��������ABC��������
�൱��ABC��ֱ�������Σ�����ACB=90��ʱ��S�����ֵ��
��ʱ��S=3S��ABC=3�� ![]() ��3��4=18
��3��4=18
����������1���������ε����ʿ��Եó�AC=DC��BC=FC����ACB=��DCF=90�㣬�Ϳ��Եó���ABC�ա�DFC���ó����ۣ���2����ͼ3������A��AP��BC�ڵ�P������D��DQ��FC��FC���ӳ����ڵ�Q��ͨ��֤����APC�ա�DQC����DQ=AP���ó����ۣ���3����ͼ 1�����ݣ�2�����Եó�S=3S��ABC �� ҪʹS���ҪʹS��ABC�����AVB=90��ʱS��ABC��Ϳ���������ۣ�

 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д� ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�