题目内容
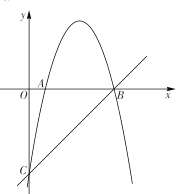
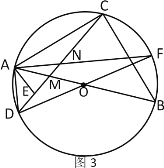
【题目】如图,矩形![]() 在平面直角坐标系中,
在平面直角坐标系中, ![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 动点
动点![]() 从原点出发,以每秒 1 个单位长度的速度沿
从原点出发,以每秒 1 个单位长度的速度沿![]() 轴正方向移动,移动时间为
轴正方向移动,移动时间为![]() 秒,过点 P 作垂直于
秒,过点 P 作垂直于![]() 轴的直线
轴的直线![]() ,交
,交![]() 于点 M ,交
于点 M ,交![]() 或
或![]() 于点 N ,直线
于点 N ,直线![]() 扫过矩形
扫过矩形![]() 的面积为
的面积为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 移动过程中到点
移动过程中到点![]() 之前的
之前的![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在直线![]() 移动过程中,第一象限的直线
移动过程中,第一象限的直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 是等腰直角三角形? 若存在,直接写出点
是等腰直角三角形? 若存在,直接写出点![]() 的坐标;若不存在,说明理由
的坐标;若不存在,说明理由
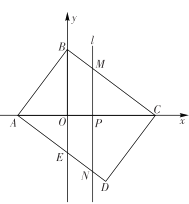
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在
;(3)存在![]() .
.
【解析】
(1)由 ![]() ,且AB=6即可求出AO的长,再由勾股定理即可求出BO的长,即可求出A和B点坐标.
,且AB=6即可求出AO的长,再由勾股定理即可求出BO的长,即可求出A和B点坐标.
(2)P点从原点出发,在到达终点前,直线l扫过的面积始终为平行四边形BMNE,故求该平行四边的底BE和高OP,相乘即得到面积S;由![]() ,且AB=6,可求出AC=10,过D点作DF⊥x轴,易证
,且AB=6,可求出AC=10,过D点作DF⊥x轴,易证![]() ,求出CF=AO,进而求出OF的长;由
,求出CF=AO,进而求出OF的长;由![]() ,故
,故![]() ,求出OE的长,进而求出OB+OE=BE.
,求出OE的长,进而求出OB+OE=BE.
(3)分类讨论,当B为直角顶角时,过Q1点作QH⊥y轴,此时△Q1HB≌△BOC,即可求出Q1的坐标;当Q2为直角顶角时,过Q2点作QM⊥y轴,QN⊥x轴,此时Q2MB≌Q2NC,即可求出Q2的坐标.
解:(1)由题意可得![]()
![]()
![]()
故答案为:![]()
(2)过点![]() 作
作![]() 轴,垂足为 F ,则
轴,垂足为 F ,则![]()
![]()
![]() ∴
∴![]()
![]()
∵![]()
∴![]() ,故
,故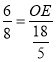 ,求得
,求得![]()
![]() .
.
当![]() 时,直线
时,直线![]() 扫过的图形是平行四边形,
扫过的图形是平行四边形,
![]()
故答案为:![]() .
.
存在,![]() .如下图所示:
.如下图所示:
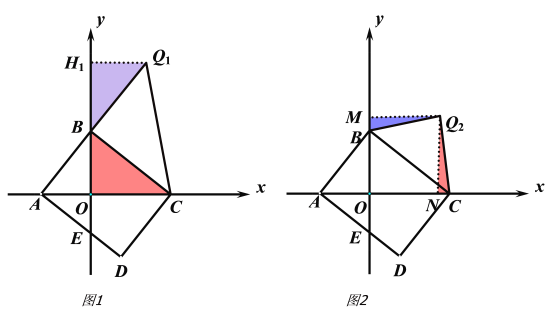
情况一:当B为直角顶角时,此时BQ1=BC,过Q1点作Q1H1⊥y轴于H1,
∴∠Q1H1B=∠BOC=90°,且BQ1=BC,
∵∠Q1BC=90°
∴∠H1BQ1+∠OBC=90°
又∠BCO+∠OBC=90°
∴∠H1BO1=∠BCO
在△Q1H1B和△BOC中:
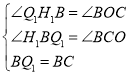 ,∴△△Q1H1B≌△BOC(AAS)
,∴△△Q1H1B≌△BOC(AAS)
∴Q1H1=BO=![]() ,BH1=OC=
,BH1=OC=![]() ,∴OH1=
,∴OH1=![]()
∴![]()
情况二:当Q2为直角顶角时,此时有Q2B=Q2C,
过Q2点分别作Q2M⊥y轴,Q2N⊥x轴
∴∠MQ2B+∠BQ2N=90°
又∴∠NQ2C+∠BQ2N=90°
∴∠MQ2B =∠NQ2C
在△MQ2B和△NQ2C中
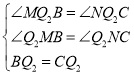 ,∴△MQ2B≌△NQ2C(AAS)
,∴△MQ2B≌△NQ2C(AAS)
∴MQ2= NQ2=OM=ON,且∠MON=90°
∴四边形Q2MON为正方形,设MB=NC=a
则OC-a=ON=OB=![]() ,且OC=
,且OC=![]()
∴求得a=![]() ,∴ON=OM=OB+a=
,∴ON=OM=OB+a=![]()
∴![]()
故答案为:![]() 和
和![]()

 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案【题目】某校九年级( 3 )班全体学生 2019 年初中毕业体育考试的成绩统计如下表:
成绩 | 35 | 39 | 42 | 43 | 45 | 49 | 50 |
人数 | 3 | 5 | 6 | 6 | 8 | 7 | 5 |
根据上表中的信息判断,下列结论中错误的是 ( )
A.该班一共有 40 名同学B.该班学生这次考试成绩的众数是 45 分
C.该班学生这次考试成绩的中位数是 44 分D.该班学生这次考试成绩的平均数是 45 分