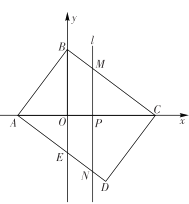
题目内容
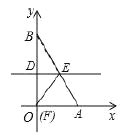
【题目】对于题目:在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 且平行
且平行![]() 轴的直线与过点
轴的直线与过点![]() 且平行
且平行![]() 轴的直线相交于点
轴的直线相交于点![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有唯一公共点,求
有唯一公共点,求![]() 的取值范围.甲的计算结果是
的取值范围.甲的计算结果是![]() ;乙的计算结果是
;乙的计算结果是![]() ,则( )
,则( )
A.甲的结果正确B.乙的结果正确
C.甲与乙的结果合在一起正确D.甲与乙的结果合在一起也不正确
【答案】D
【解析】
首先求出A、B、C三点的坐标,以及抛物线的顶点坐标和对称轴,因为不清楚![]() 的取值,所以分两种情况进行讨论,进而求得
的取值,所以分两种情况进行讨论,进而求得![]() 的取值范围.
的取值范围.
解:对于直线![]() ,令y=0,解得x=5;
,令y=0,解得x=5;
令x=0,得y=4,
∴ A(5,0)、B(0,4),
∵过点![]() 且平行
且平行![]() 轴的直线与过点
轴的直线与过点![]() 且平行
且平行![]() 轴的直线相交于点
轴的直线相交于点![]() ,
,
∴![]() (5,4),
(5,4),
∵ ![]() =
=![]() 2-4
2-4![]() ,
,
∴ 抛物线的顶点坐标为(1,-4![]() ),抛物线的对称轴为
),抛物线的对称轴为![]() ,
,
当抛物线![]() 与线段BC有唯一公共点时,分两种情况:
与线段BC有唯一公共点时,分两种情况:
① 当![]() 时,如图:
时,如图:

由图可得:25![]() -10
-10![]() -3
-3![]() ,
,
解得:![]() ;
;
② 当![]() 时,如图
时,如图
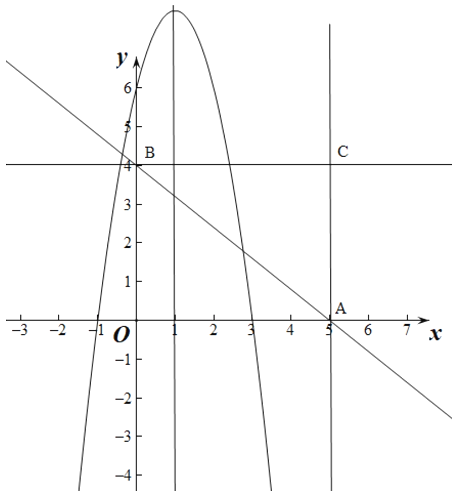
抛物线![]() 与
与![]() 轴的交点坐标为(0,-3
轴的交点坐标为(0,-3![]() ),抛物线的对称轴与直线BC的交点坐标为(1,-4),
),抛物线的对称轴与直线BC的交点坐标为(1,-4),
由图可得: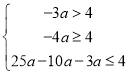 ,
,
解得:![]()
综上所述,![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
故选C.

【题目】随着人们生活质量的提高,越来越多的人们关注运动与健康,近来“微信运动”逐渐被大家关注和喜爱.某兴趣小组为了了解某社区居民的“微信运动”情况,进行了随机抽样调查,对他们一日“微信运动”中的步数进行了统计,下面给出部分信息:
①
| 频数 | 频率 |
| 5 |
|
| 10 | 0.2 |
| 15 | 0.3 |
|
| 0.2 |
| 8 | 0.16 |
| 2 | 0.04 |
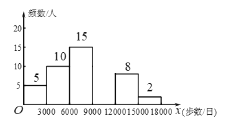
![]() 这一组的数据为:
这一组的数据为:
6000 6200 6200 6500 6600 6800 7000 7200 7200 7200 7800 8000 8300 8700 8900
根据以上信息,回答下列问题:
(1)本次被调查的居民有__________人:表中![]() ______________,
______________,![]() ___________;
___________;
(2)补全频数分布直方图;
(3)直接写出被调查的居民在“微信运动”中步数的中位数;
(4)本社区约有5000人,用调查样本估计一日步数不低于9000步的人数.