题目内容
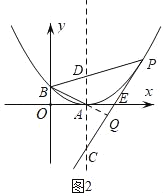
【题目】如图1,抛物线y=![]() (x﹣m)2的顶点A在x轴正半轴上,交y轴于B点,S△OAB=1.
(x﹣m)2的顶点A在x轴正半轴上,交y轴于B点,S△OAB=1.

(1)求抛物线的解析式;
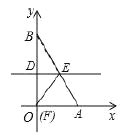
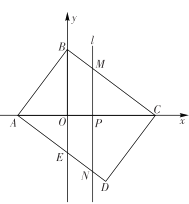
(2)如图2,P是第一象限内抛物线上对称轴右侧一点,过P的直线l与抛物线有且只有一个公共点,l交抛物线对称轴于C点,连PB交对称轴于D点,若∠BAO=∠PCD,求证:AC=2AD;
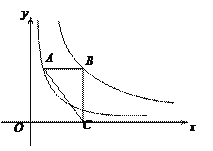
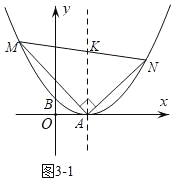
(3)如图3,以A为顶点作直角,直角边分别与抛物线交于M、N两点,当直角∠MAN绕A点旋转时,求证:MN始终经过一个定点,并求出该定点的坐标.
【答案】(1)y=![]() x2﹣x+1;(2)见解析;(3)定点K的坐标为(2,4)
x2﹣x+1;(2)见解析;(3)定点K的坐标为(2,4)
【解析】
(1)先确定A、B的坐标,然后运用顶点式的待定系数法即可解答;
(2)由(1)得抛物线对称轴为直线x=2.D、C两点在直线x=2上,则设C(2,n),D(2,n');延长BA交直线PC于点Q并设直线PC交x轴于点E.再说明Rt△BOA∽Rt△EAC,进一步可得AC=2AE;然后再说明BQ⊥PC,再求出AB、PC、PB的解析式,最后结合图形即可解答;
(3)过A作垂直于x轴的直线并交MN于点K(2,k),然后再根据旋转的性质设出M(2﹣k,k),最后代入y=![]() (x﹣2)2即可求得k的值,进而确定该点的坐标.
(x﹣2)2即可求得k的值,进而确定该点的坐标.
解:(1)由题意和y=![]() (x﹣m)2设A(m,0)
(x﹣m)2设A(m,0)
当x=0时,y═![]() (0﹣m)2=
(0﹣m)2=![]() ,即设B(0,
,即设B(0,![]() )
)
∴OA=m,OB=![]()
由S△OAB=1
∴![]() OAOB=1,即m
OAOB=1,即m![]() =2
=2
解得,m=2
∴A(2,0),B(0,1)
把y=![]() (x﹣2)2化为一般式为,y=
(x﹣2)2化为一般式为,y=![]() x2﹣x+1.
x2﹣x+1.
(2)由(1)得抛物线对称轴为直线x=2.
D、C两点在直线x=2上,则设C(2,n),D(2,n')
如图2延长BA交直线PC于点Q并设直线PC交x轴于点E.
∵∠BAO=∠PCD,∠BOA=∠EAC=90°
∴Rt△BOA∽Rt△EAC
∴∠BAO=∠ECA
∴tan∠BAO=tan∠ECA=![]()
∴![]() =
=![]()
∴AC=2AE
又∵∠BAO=∠EAQ,∠BAO=∠ECA
∴∠ECA=∠EAQ
又∵∠ECA+∠CEA=90°
∴∠EAQ+∠QEA=90°
∴BQ⊥PC
设直线AB的解析式为y=kx+b,把A(2,0),B(0,1)代入得,
![]() 解得
解得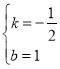
∴直线AB的解析式为,y=﹣![]() x+1
x+1
由BQ⊥PC设直线PC的解析式为y=2x+b'.
又∵过P的直线l与抛物线有且只有一个公共点
∴令2x+b'═![]() (x﹣2)2
(x﹣2)2
整理得,x2﹣12x+4﹣4b'=0,且△=0
即144﹣4(4﹣4b')=0
解得,b'=﹣8
∴直线PC的解析式为,y=2x﹣8.
∴把点C(2,n)代入y=2x﹣8中得,n=2×2﹣8
解得,n=﹣4.
∴C点坐标为(2,﹣4),即AC=4
由AC=2AE得,AE=2.
把b’=﹣8代入方程x2﹣12x+4﹣4b'=0中得,
x2﹣12x+36=0
解得,x1=x2=6
再把x=6代入y=2x﹣8中得,y=2×6﹣8
解得,y=4
∴P(6,4)
设直线PB解析式为y=k'x+1
把P(6,4)代入上式得,4=6k'+1
解得,k'=![]()
∴直线PB的解析式为,y=![]() x+1
x+1
又∵D(2,n')在直线PB上,将其代入y=![]() x+1中得,
x+1中得,
n'=![]() ×2+1=2
×2+1=2
∴D点坐标为(2,2),即AD=2
∴AD=AE
∴AC=2AD
(3)如图3﹣1过A作垂直于x轴的直线并交MN于点K(2,k).
∵∠MAN为直角
∴∠M+∠N=90°,∠MAK+NAK=90°
又∵∠MKA=∠N+∠NAK,∠NKA=∠M+MAK
∴∠MKA+∠NKA=180°
∴直角∠MAN绕A点旋转时,M、K、N三点始终在一条直线上,即MN始终经过一个定点K.
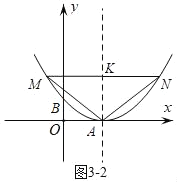
如图3﹣2当MN∥y轴时,此时Rt△MAN为等腰直角三角形,应有AK=MK,则设M(2﹣k,k).
把M(2﹣k,k)代入y=![]() (x﹣2)2中得,k=
(x﹣2)2中得,k=![]() (2﹣k﹣2)2
(2﹣k﹣2)2
解得,k1=0(舍去),k2=4
∴定点K的坐标为(2,4).

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案