题目内容
【题目】已知:AB为⊙O的直径,点C为弧AB的中点,点D为⊙O上一点,连接CD,交AB于点M,AE为∠DAM的平分线,交CD于点E.
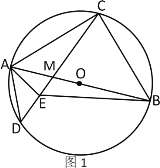
(1)如图1,连接BE,若∠ACD=22°,求∠MBE的度数;
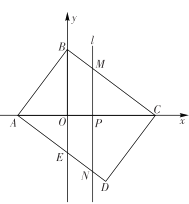
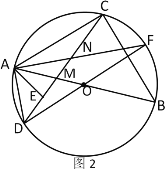
(2) 如图2,连接DO并延长,交⊙O于点F,连接AF,交CD于点N.
①求证:DM2+CN2=CM2;
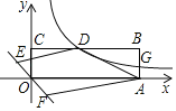
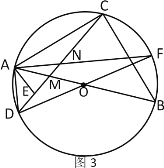
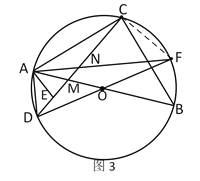
②如图3,当AD=1,AB=![]() 时,请直接写出线段ME的长.
时,请直接写出线段ME的长.
【答案】(1)![]() ;(2)①见解析;②
;(2)①见解析;②![]()
【解析】
(1)由圆周角定理,得到∠CAB=∠ABC=∠ADC= 45°,由角平分线的定义和三角形的外角性质,得到∠CAE=∠CEA,结合等腰三角形的性质和三角形的内角和定理,即可求出答案;
(2)①根据题意,将△ADM绕点A逆时针旋转90°,得到![]() ,连接
,连接![]() ,由旋转的性质,△ADM≌△
,由旋转的性质,△ADM≌△![]() ,得到DM=
,得到DM=![]() ,然后证明△
,然后证明△![]() AC≌△MAC,得到
AC≌△MAC,得到![]() =CM,利用勾股定理,即可得到结论成立;
=CM,利用勾股定理,即可得到结论成立;
②连接CF,由(1)可知AC=BC=CE,根据等腰直角三角形的性质和勾股定理求出CE的长度,然后利用相似三角形的判定和性质,得到线段的比,然后构建方程,求出CM的长度,即可得到ME的长度.
(1)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵点C为弧AB中点,
∴![]() =
=![]() ,
,
∴∠CAB=∠ABC=∠ADC= 45°,AC=BC
∴△ACB是等腰直角三角形
∵![]() ∠DAM的平分线,
∠DAM的平分线,
∴∠MAE=∠EAD
∵∠CAE=∠CAB+∠MAE,∠CEA=∠ADC+∠EAD,
∴∠CAE=∠CEA,
∴AC=CE=BC
∴∠CBE=∠CBM+∠MBE=![]()
∵∠ACD=22°,
![]()
又∵∠CBM=45°
∴∠MBE=![]() ;
;
(2)证明:将△ADM绕点A逆时针旋转90°,得到![]() ,连接
,连接![]() ,
,
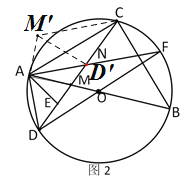
∵DF是⊙O的直径,
∴∠DAF=90°
∵∠ADC=45°
∴△AND为等腰三角形,AD=AN
∴![]() 和AN重合
和AN重合
∴△ADM≌△ANM’
∴DM=![]() ,AM=
,AM=![]() ,∠
,∠![]() =∠ADC=45°,
=∠ADC=45°,
∵∠M’ AM=90°,∠CAB=45°,
∴∠![]() =45°
=45°
∴△M’ AC≌△MAC(SAS),
∴![]() =CM
=CM
∵∠M’NA=∠ADC=∠AND=45°,
∴∠M’ND=∠M’NC=90°,
∴M’ N2+ CN 2=C M’ 2,
∴MD2+ CN 2=C M2 ;
(3)如图:连接CF,
∵AB与DF为直径,AB=![]() ,AD=1,
,AD=1,
∴∠DCF=90°,∠DAF=90°,
∴![]() ,
,
由(1)可知,△AND是等腰直角三角形,△ABC是等腰直角三角形,
∴AN=AD=1,∠AND=45°,AC=BC=CE=![]() ,
,
∴NF=3-1=2,
∴△CNF是等腰直角三角形,
∴CN=CF=![]() ,
,
∴![]() ,
,
∵∠AMD=∠CMB,∠ADM=∠CBM=45°,
∴△ADM∽△CBM,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案