题目内容
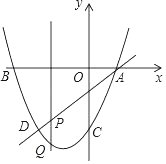
【题目】如图,抛物线y=x2+bx﹣3过点A(1,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P是线段AD上的动点.
(1)b= ,抛物线的顶点坐标为 ;
(2)求直线AD的解析式;
(3)过点P的直线垂直于x轴,交抛物线于点Q,连接AQ,DQ,当△ADQ的面积等于△ABD的面积的一半时,求点Q的坐标.
【答案】(1)2 (﹣1,﹣4);(2)y=x﹣1;(3)Q(0,﹣3)或(﹣1,﹣4).
【解析】
(1)将点A的坐标代入函数解析式求得b的值,然后利用配方法将函数解析式转化为顶点式,可以直接求得顶点坐标;
(2)结合(1)中抛物线解析式求得点D的坐标,利用点A、D的坐标来求直线AD解析式;
(3)由二次函数图象上点的坐标特征求得点B的坐标,易得AB=4.结合三角形面积公式求得S△ABD=6.设P(m,m﹣1),Q(m,m2+2m﹣3).则PQ=﹣m2﹣m+2.利用分割法得到:S△ADQ=S△APQ+S△DPQ=![]() PQ=
PQ=![]() (﹣m2﹣m+2).根据已知条件列出方程
(﹣m2﹣m+2).根据已知条件列出方程![]() (﹣m2﹣m+2)=3.通过解方程求得m的值,即可求得点Q的坐标.
(﹣m2﹣m+2)=3.通过解方程求得m的值,即可求得点Q的坐标.
解:(1)把A(1,0)代入y=x2+bx﹣3,得12+b﹣3=0.
解得b=2.
故该抛物线解析式为:y=x2+2x﹣3=(x+1)2﹣4,即y=(x+1)2﹣4.
故顶点坐标是(﹣1,﹣4).
故答案是:2;(﹣1,﹣4).
(2)由(1)知,抛物线解析式为:y=x2+2x﹣3.
当x=﹣2,则y=(﹣2)2+2×(﹣2)﹣3=﹣3,
∴点D的坐标是(﹣2,﹣3).
设直线AD的解析式为:y=kx+t(k≠0).
把A(1,0),D(﹣2,﹣3)分别代入,得![]() .
.
解得![]() .
.
∴直线AD的解析式为:y=x﹣1;
(3)当y=0时,x2+2x﹣3=0,
解得x1=1,x2=﹣3,
∴B(﹣3,0),
∴AB=4.
∴S△ABD=![]() ×4×3=6.
×4×3=6.
设P(m,m﹣1),Q(m,m2+2m﹣3).
则PQ=(m﹣1)﹣(m2+2m﹣3)=﹣m2﹣m+2.
∴S△ADQ=S△APQ+S△DPQ=![]() PQ(1﹣m)+
PQ(1﹣m)+![]() PQ(m+2)=
PQ(m+2)=![]() PQ=
PQ=![]() (﹣m2﹣m+2).
(﹣m2﹣m+2).
当△ADQ的面积等于△ABD的面积的一半时,![]() (﹣m2﹣m+2)=3.
(﹣m2﹣m+2)=3.
解得m1=0,m2=﹣1.
∴Q(0,﹣3)或(﹣1,﹣4).

 阅读快车系列答案
阅读快车系列答案