题目内容
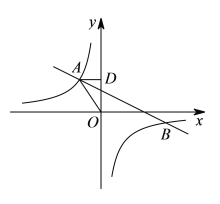
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的延长线上一点,且∠PDB=
的延长线上一点,且∠PDB=![]() ∠A,连接
∠A,连接![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)填空:
①当![]() 的度数为______时,四边形
的度数为______时,四边形![]() 是菱形;
是菱形;
②当![]() 时,
时,![]() 的面积为_________.
的面积为_________.
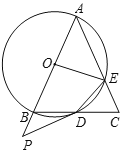
【答案】(1)证明见解析;(2)①30°;②![]()
【解析】
(1)要证明切线,按照圆周角定理和已知的2倍角关系,证明∠ODP为直角
(2)当四边形OBDE为菱形时,△OBD为等边三角形,则∠P为30°
(3)连接AD,过点E作BC的垂线,通过平行相似得到a、b的第一种关系,根据勾股定理得到a、b的第二种关系,用a、b表示出△CDE的面积,再代入a与b的关系,获得面积值.
(1)如图,连接OD
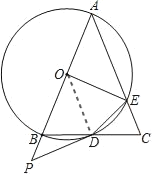
∵OB=OD,∠PDB=![]() ∠A
∠A
∴∠ODB=∠ABD=90°﹣![]() ∠A=90°﹣∠PDB
∠A=90°﹣∠PDB
∴∠ODB+∠PDB=90°
∴∠ODP=90°
又∵OD是⊙O的半径
∴PD是⊙O的切线
(2)①30°
若四边形OBDE为菱形,则OB=BD=DE=EO=OD
∴△OBD为等边三角形
∴∠ABD=∠A=60°
∴∠PDB=30°
∴∠P=30°
即当∠P为30°时,四边形OBDE为菱形
②![]()
如图所示
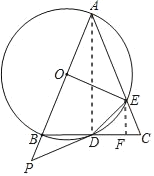
∵AO=OE=2,∠AOE=90°
∴AE=![]()
∴EC=4﹣![]()
∵∠BAC=45°
∴∠EDB=135°
∴∠EDC=45°
设DF=EF=b,FC=a
∵△EFC∽△ADC
∴![]()
∴![]()
∵a2+b2=(4﹣![]() )2
)2
解得![]()
![]() .
.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目