题目内容
【题目】在矩形OABC中,OA=4,OC=2,以点O为坐标原点,OA所在的直线为x轴,建立直角坐标系.
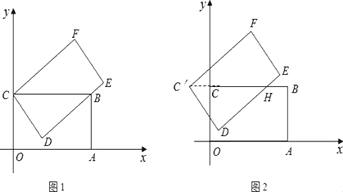
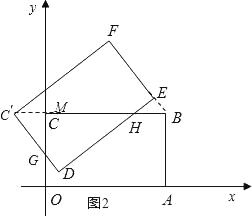
(1)将矩形OABC绕点C逆时针旋转至矩形DEFC,如图1,DE经过点B,求旋转角的大小和点D,F的坐标;
(2)将图1中矩形DEFC沿直线BC向左平移,如图2,平移速度是每秒1个单位长度.
①经过几秒,直线EF经过点B;
②设两矩形重叠部分的面积为S,运动时间为t,写出重叠部分面积S与时间t之间的函数关系式.
【答案】(1)旋转角为30°,D(1,![]() ),F(
),F(![]() ;(2)①直线EF经过点B时所需的时间为
;(2)①直线EF经过点B时所需的时间为![]() 秒;②当0<t<1时,
秒;②当0<t<1时,![]() ;当1≤t<4时,
;当1≤t<4时,![]() .
.
【解析】
(1)根据OA=4,OC=2,可得BC=2CD,则可以求出∠BCD=60°,则旋转角即可求得;作DM⊥CB于点M,FN⊥CB于点N,根据三角函数即可求得DM,CM的长,从而求得D的坐标,在Rt△CFN中,根据三角函数求得CN,FN的长,即可得F的坐标;
(2)①如图,HB即为直线EF经过点B时移动的距离,在Rt△C′DH中利用三角函数即可求得DH,从而得到HE,再在Rt△HEB中,利用三角函数求得BH,即可求得时间;
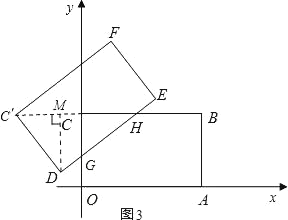
②分两种情况进行讨论:当0<t<1时,重叠部分面积为四边形DGCH,如图2;当1≤t<4时,重叠部分的面积为△GCH,如图3,分别求解即可.
解:(1)如图1,在矩形OABC中,OA=4,OC=2,
∴在Rt△BCD中,BC=2CD,即![]() ,
,
∴∠BCD=60°,
∴旋转角∠OCD=30°,
作DM⊥CB于点M,FN⊥CB于点N,
在Rt△CDM中,CM=CDcos60°=1,DM=CDsin60°=![]() ,
,
∴点D到x轴的距离为![]() ,
,
在Rt△CFN中,![]() ,
,
∴点F到x轴的距离为4,
故D(1,![]() ),F(
),F(![]() ,
,![]() );
);
(2)①如图2,HB即为直线EF经过点B时移动的距离,
在Rt△C′DH中,![]() ,
,
∴![]() ,
,
在Rt△BEH中,∠BHE=∠C′HD=30°,cos30°=![]() ,则
,则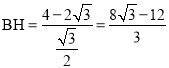 ,
,
∴直线EF经过点B时所需的时间为![]() 秒;
秒;
②过点D作DM⊥BC于点M,
在Rt△DMC′中,C′M=![]() ,
,
当0<t<1时,重叠部分面积为四边形DGCH,如图2,
∵C′C=t,CG=C′C·tan60°=![]() ,
,
∴![]() ,
,
当1≤t<4时,重叠部分的面积为△GCH,如图3,
∵![]() ,
,
∴![]() .
.