题目内容
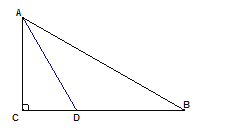
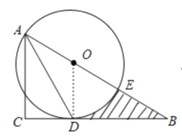
【题目】已知,如图,在Rt△ABC中,∠C=90,∠BAC的角平分线AD交BC边于D.
(1)以AB边上一点O为圆心作⊙O,使它过A,D两点(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由;
(2)若(1)中的⊙O与AB边的另一个交点为E,AB=3![]() ,BD=3,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和
,BD=3,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和![]() )
)
【答案】(1)相切,理由见解析; (2)![]()
【解析】
(1)因为⊙O过A,D两点,故圆心O应在AD垂直平分线上,根据尺规作图法,作AD垂直平分线,与AB的交点即为O点,根据等边对等角和角的等量代换可得∠CAD=∠ODA ,继而可知AC∥OD,再根据“两直线平行,内错角相等”和切线判定定理,即可求证.
(2)设⊙O的半径为x,根据勾股定理,列关于x的方程,求x的值,再根据S阴影部分=S△ODB-S扇形ODE,求出S阴影部分即可.
(1)作图如图所示.
直线BC与⊙O的位置关系为相切.
理由:连接OD,
∵OA=OD,
∴∠OAD=∠ODA
∵AD是∠OAC的角平分线,
∴∠OAD=∠CAD,
∴∠CAD=∠ODA,
∴AC∥OD,
∴∠ODB=∠ACB=90°
∴OD⊥BC
即OD为⊙O的切线;
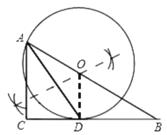
(2)如图所示,阴影部分的面积即为所求面积.
设⊙O的半径为x,
∵AB=3![]() ,OD=OA=x,
,OD=OA=x,
∴OB=3![]() -x,
-x,
在Rt△ODB中,BD=3,OD=x,OB=3![]() -x
-x
根据勾股定理得:
![]()
![]() ,
,
解得:x=![]()
即OD=![]()
OB=![]()
∴sin∠B=![]()
∴∠B=30°
∴∠BOD=90°-30°=60°
∴S阴影部分=S△ODB-S扇形ODE=![]() OD×BD-
OD×BD-![]() =
=![]()

【题目】参照学习函数的过程与方法,探究函数![]()
![]() 的图象与性质.因为
的图象与性质.因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究.
来探究.
列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点:在平面直角坐标系中,以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
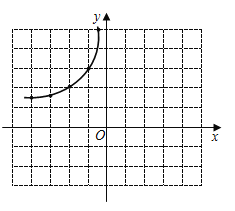
(1)请补全函数图象;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而_________;(填“增大”或“减小”)
的增大而_________;(填“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向________平移________个单位而得到;
的图象向________平移________个单位而得到;
③图象关于点_________中心对称.(填点的坐标)
(3)结合函数图象,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.