题目内容
【题目】在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在线段BC上,且AE=CF,连接EF.
(1)如图,已知线段AB,请补全图形,画出符合题意的图形.
(2)求证:BE=BF.
(3)若∠EAC=30°,则∠CFE是多少度?
![]()
【答案】(1)作图见解析;(2)证明见解析;(3)15°
【解析】
(1)根据题意作图即可;
(2)可根据“HL”判断Rt△ABE≌Rt△CBF,则可得到BE=BF;
(3)由AB=CB,∠ABC=90°,可判断△ABC为等腰直角三角形,则∠BAC=∠BCA=45°,可得到∠BAE=15°,再根据Rt△ABE≌Rt△CBF得到∠BCF=∠BAE=15°,BE=BF,进而得出∠FEB=45°,进而解答即可.
解:(1)如图,根据题意画图,
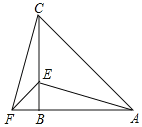
(2)∵∠ABC=90°=∠FBC,
∴在Rt△ABE和Rt△CBF中,
![]() ,
,
∴Rt△ABE≌Rt△CBF(HL),
∴BE=BF;
(2)∵AB=CB,∠ABC=90°,
∴∠BAC=∠BCA=45°,
∵∠CAE=30°,
∴∠BAE=45°﹣30°=15°,
∵Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°,BE=BF,
∴△BEF是等腰直角三角形,
∴∠FEB=45°,
∴∠CFE=45°﹣30°=15°.

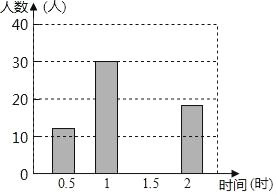
【题目】某校倡议八年级学生利用双休日在各自社区参加义务劳动.为了了解同学们参加义务劳动的时间,学校随机调查了部分同学参加义务劳动的时间,用得到的数据绘制成如下不完整的统计图表:
劳动时间(时) | 频数(人) | 频率 |
0.5 | 12 | 0.12 |
1 | 30 | 0.3 |
1.5 | x | 0.4 |
2 | 18 | y |
合计 | m | 1 |
(1)统计表中的m=_____,x=______,y=_______;
(2)请将频数分布直方图补充完整;
(3)求被调查同学的平均劳动时间.