题目内容
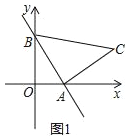
【题目】一次函数y=﹣2x+2的图象与x轴、y轴分别交于点A,B.在y轴左侧有一点P(﹣1,a).
(1)如图1,以线段AB为直角边在第一象限内作等腰Rt△ABC,且∠BAC=90°,求点C的坐标;
(2)当a=![]() 时,求△ABP的面积;
时,求△ABP的面积;
(3)当a=﹣2时,点Q是直线y=﹣2x+2上一点,且△POQ的面积为5,求点Q的坐标.
【答案】(1)C(3,1);(2)S△ABP=![]() ; (3)点Q的坐标为(﹣2,6)或(3,﹣4).
; (3)点Q的坐标为(﹣2,6)或(3,﹣4).
【解析】试题分析: ![]() 过点C作
过点C作![]() 轴于D,根据一次函数解析式求得
轴于D,根据一次函数解析式求得![]() 证明
证明![]() ≌
≌![]() 得到
得到![]() 即可求得点
即可求得点![]() 的坐标.
的坐标.
![]() 连接PO,根据
连接PO,根据![]() 即可求得.
即可求得.
![]() 分成三种情况进行讨论.
分成三种情况进行讨论.
试题解析:(1)如图1,过点C作![]() 轴于D,
轴于D,

令x=0,得y=2,
令y=0,得x=1,
∴![]()
∴![]()
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]() ≌
≌![]()
∴![]()
∴![]()
∴![]()
(2)连接PO,如图2,
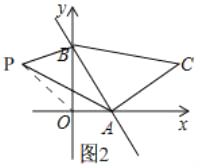
![]()
![]()
(3)设点![]()
①当点Q在第二象限时,
如图3,作![]() 轴于M,
轴于M, ![]() 轴于N,
轴于N,

![]()
∵S△POQ=S梯形PMNQ﹣S△ANQ﹣S△AMP
![]()
∴m=﹣2,
∴![]()
∴点![]() 符合题意;
符合题意;
②点Q在第一象限时,如图4,
作![]() 轴,
轴, ![]() 轴于N,PM交MN于点M,
轴于N,PM交MN于点M,

![]() ∴QN=﹣2m+4,
∴QN=﹣2m+4,
∴S△POQ=S△OQN+S梯形ONMP﹣S△QMP
![]()
∴m=3,
∴![]()
∴![]() 但不在第一象限,不符合题意,舍去;
但不在第一象限,不符合题意,舍去;
③当点Q在第四象限时,如图5,
作![]() 轴于M,
轴于M, ![]() 轴于N,
轴于N,
∴![]()
∴S△POQ=S梯形PMNQ﹣S△PMO﹣S△QNO
![]()
∴![]()
∴![]()
∴Q![]() 符合题意,
符合题意,
即:点Q的坐标为![]() 或
或![]()


练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目