题目内容
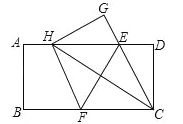
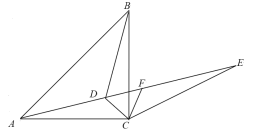
【题目】如图,已知在△ABC中,∠ACB=90°,AC=BC,∠CAD=∠CBD.
(1)求证:CD平分∠ACB;
(2)点E是AD延长线上一点,CE=CA,CF∥BD交AE于点F,若∠CAD=15°,
求证:EF=BD.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据等腰直角三角形的性质可得∠BAC=∠ABC,进而得到∠BAD=∠ABD,由等角对等边可得DA=DB,利用SSS证明△DAC≌△DBC,得到∠DCA=∠DCB即可得出结论;
(2)根据△DAC≌△DBC,CE=CA可得∠DBC=∠E=15°,CE=CA=CB,然后根据三角形外角的性质求出∠BDF=60°,利用平行线的性质得出∠CFD=60°,可得∠CFE=120°,再根据三角形内角和定理求出∠CDB=120°,利用AAS证明△BDC≌△EFC即可得出结论.
证明:(1)∵∠ACB=90°,AC=BC,
∴∠BAC=∠ABC=45°,
∵∠CAD=∠CBD,
∴∠BAD=∠ABD,
∴DA=DB,
又∵AC=BC,CD=CD,
∴△DAC≌△DBC,
∴∠DCA=∠DCB,即CD平分∠ACB;
(2)∵△DAC≌△DBC,CE=CA,∠CAD=15°,
∴∠DBC=15°,∠E=15°,CE=CA=CB,
∴∠BAD=∠ABD=45°-15°=30°,
∴∠BDF=30°+30°=60°,
∵CF∥BD,
∴∠CFD=∠BDF=60°,
∴∠CFE=120°,
又∵CD平分∠ACB,
∴∠DCB=45°,
∴∠CDB=180°-15°-45°=120°,
在△BDC和△EFC中,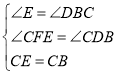 ,
,
∴△BDC≌△EFC(AAS),
∴EF=BD.

练习册系列答案
相关题目